Bài giảng này thuộc Khóa ôn thi ĐH 2013. Thảo luận và đặt câu hỏi tại đây
- Xem bài giảng I.1 - I.2 - I.3 - I.4

$\quad$ Việc giải và biện luận phương trình, bất phương trình, hệ phương trình, hệ bất phương trình,...bằng các phương pháp như: Biến đổi tương đương, đặt ẩn phụ, lượng giác hóa, hình học,...khá quen thuộc đối với các bạn chuẩn bị thi vào đại học. Tuy nhiên đối mặt với một bài toán dạng này các bạn ít nhiều còn lúng túng, chưa tìm được lời giải hoặc xác định được đường lối nhưng lại không đưa ra được kết quả cuối cùng!
$\quad$ Trong phạm vi bài giảng này tôi muốn bàn về một phương pháp để giải quyết các bài toán về phương trình, bất phương trình, hệ phương trình và hệ bất phương trình,...khi mà các phương pháp nêu trên gặp khó khăn hoặc bế tắc! Đó là "Ứng dụng tính đơn điệu của hàm số".
Tính chất 1: Giả sử hàm số $f(x)$ liên tục và đơn điệu trên tập $D$ thì phương trình $f(x)=0$ có nhiều nhất một nghiệm thuộc $D$.
Tính chất 2: Nếu phương trình $f'(x)=0$ có một nghiệm trên tập $(a,b)$ thì phương trình $f(x)=0$ có nhiều nhất hai nghiệm trên $(a,b)$.
Tính chất 3: Nếu $f(x)$ liên tục, đồng biến trên $D$ và $g(x)$ liên tục, nghịch biến (hoặc hàm hằng) trên $D$ thì phương trình $f(x)=g(x)$ có nhiều nhất một nghiệm trên $D$.
Tính chất 4: Nếu hàm số $f(x)$ liên tục và đơn điệu trên $D$ thì với $\forall {u},{v} \in D$ ta có: $f(u)=f(v) \Leftrightarrow u=v$.
Tính chất 5: Nếu $f(x)$ đơn điệu trên $(a,b)$ thì $x,y,z \in (a,b)$ là nghiệm của hệ phương trình:
$$\left\{ \begin{gathered} f(x) = y \\ f(y) = z \\ f(z) = x \\ \end{gathered} \right. \Leftrightarrow x = y = z$$
Tính chất 6: $f(x)$ đồng biến trên $(a,b)$ thì $f(u) < f(v ) \Leftrightarrow u < v$
$f(x)$ nghịch biến trên $(a,b)$ thì $f(u) v$ với mọi $u,v \in (a,b)$.
$\quad$ Chỉ cần nắm được định nghĩa về hàm số đồng biến, nghịch biến các bạn dễ dàng suy ra tính chất 1, 2, 3, 4 và 6. Riêng tính chất 5 SGK không đề cập, do đó mỗi khi sử dụng kết quả này các bạn phải chứng minh lại. Tôi sẽ nói chi tiết hơn và đồng thời chứng minh tính chất này trong Ví dụ 2.2 của Vấn đề 2!

Vấn đề 1. Ứng dụng tính đơn điệu của hàm số để giải phương trình
Ví dụ 1.1. Giải các phương trình sau:
$\quad$ a) $\sqrt {4x - 1} + \sqrt {4{x^2} - 1} = 1$
$\quad$ b) $3{x^7} - \sqrt {5 - 4x} = 3 - {x^3}$
$\quad$ Nhận định: Đối với câu 1, có thể bạn nghĩ đến việc biến đổi tương đương hoặc sẽ bình phương, tuy nhiên bạn sẽ gặp khó trong biến đổi. Câu 2, các phương pháp "truyền thống" không khả thi.
$\quad$ Nếu bạn chịu khó quan sát và chuyển vế đơn giản thì vế trái đều là những hàm số đồng biến (trên một tập nào đó). Lúc này, sử dụng tính đơn điệu để giải quyết bài toán đã nảy ra trong đầu bạn. Vấn đề còn lại là đoán nghiệm! Công việc này không khó, nhưng nếu bạn cứ thử từng số thì sẽ mất thời gian. Hãy ưu tiên những giá trị của $x$ sao cho các biểu thức dưới dấu căn nhận giá trị là số chính phương!
Lời giải.
a) Điều kiện: $x \geqslant \frac{1}{2}$
Phương trình đã cho $ \Leftrightarrow \sqrt {4x - 1} + \sqrt {4{x^2} - 1} - 1 = 0$
Xét hàm số $f(x) = \sqrt {4x - 1} + \sqrt {4{x^2} - 1}- 1$ trên $[\frac{1}{2}; + \infty)$. Ta thấy rằng:
+ Hàm số $f(x)$ liên tục trên $[\frac{1}{2}; + \infty)$
+ Có đạo hàm $f'(x) = \frac{2}{\sqrt {4x-1}}+ \frac{4x}{\sqrt {4x^2-1}}> 0$ với $\forall x \in (\frac{1}{2}; + \infty)$.
Do đó hàm $f(x)$ đồng biến trên $(\frac{1}{2}; + \infty)$.
+ $f(\frac{1}{2}) = 0$
Kết luận: $x = \frac{1}{2}$ là nghiệm duy nhất của phương trình đã cho. (Xem tính chất 1!)
b) Điều kiện: $x \leqslant \frac{5}{4}$
Phương trình đã cho $ \Leftrightarrow 3{x^7} + {x^3} - \sqrt {5 - 4x} = 3$
Xét hàm số $f(x) = 3{x^7} + {x^3} - \sqrt {5 - 4x} = 3$ trên $(- \infty ;\frac{5}{4}]$. Ta thấy rằng:
+ Hàm số $f(x)$ liên tục trên $(- \infty ;\frac{5}{4}]$
+ Có đạo hàm $f'(x) = 21{x^6} + 3{x^2} + \frac{2}{{\sqrt {5 - 4x} }} > 0$ với $\forall x \in (- \infty ;\frac{5}{4})$.
Do đó hàm $f(x)$ đồng biến trên $(- \infty ;\frac{5}{4})$.
+ $f(1) = 3$
Kết luận: $x = 1$ là nghiệm duy nhất của phương trình đã cho.
Ví dụ 1.2. Giải phương trình: $\root 3 \of {x + 2}+\root 3 \of {x+1}=\root 3 \of {2x^2+1}+\root 3 \of {2x^2}$
$\quad$ Nhận định: Cũng với tư duy như trong Ví dụ 1.1 nhưng sẽ khó khẳng định được hàm số $f(x)$ liên tục, đơn điệu trên TXĐ của nó. Tuy nhiên, quan sát kỹ thì thấy các biểu thức dưới dấu căn ở 2 vế có chung một mối liên hệ:
$$x + 2 =(x + 1) + 1$$
$$ 2x^2+ 1 =(2x^2) + 1$$
Do đó, nếu đặt $u: = \root 3 \of {x + 1} $ và $v: = \root 3 \of {2x^2}$ thì phương trình đã cho trở thành:
$$u+ \root 3 \of {u^3+1}=v + \root 3 \of {v^3+1}$$
Đến đây, ta chỉ việc xét một hàm số có dạng $f(t)= t+ \root 3 \of {{t^3}+1}$ và vận dụng tính chất 4, bài toán được giải quyết!
Lời giải. Tập xác định: $\mathbb {R}$
Đặt $u: = \root 3 \of {x + 1} $ và $v: = \root 3 \of {2x^2}$ thì phương trình đã cho trở thành:
$$u+ \root 3 \of {u^3+1}=v + \root 3 \of {v^3+1} \text{ hay } f(u) = f(v)$$
Xét hàm số $f(t)= t+ \root 3 \of {{t^3}+1}$ trên $\mathbb {R}$. Ta thấy:
+ $f(t)$ là hàm liên tục trên $\mathbb R$
+ Có đạo hàm $f'(t) = 1+\frac{t^2}{\root 3 \of {(t^3+1)^2}} > 0$ trên $\mathbb R$ nên $f(t)$ là hàm đồng biến trên trên $\mathbb R$.
Do đó
$$f(u) = f(v) & \Leftrightarrow u = v$$
$$ \Leftrightarrow 2x^2= x + 1$$
Kết luận: Nghiệm của phương trình là: $x=1$ và $x = \frac{1}{2}$.
Bài tập
Bài tập 1.1. Giải các phương trình sau:
$\quad \quad $ a) $\sqrt {15 - x} + \sqrt {3 - x} = 6$
$\quad \quad $ b) $\sqrt {3x - 5} + \sqrt {2x + 3} = 2 + \sqrt {12 - x}$
$\quad \quad $ c) $\sqrt {2{x^2} + 23} = 4x - 2 + \sqrt {2{x^2} + 7}$
$\quad \quad $ d) $\sqrt {{x^2} + 15} = 3x - 2 + \sqrt {{x^2} + 8} $
$\quad \quad $ e) ${x^5} + {x^3} - \sqrt {1 - 3x} + 4 = 0$
Bài tập 1.2. Giải các phương trình sau:
$\quad \quad $ a) $8x^3- {(\sqrt {2x + 1})^3} = \sqrt {2x + 1}- 2x$
$\quad \quad $ b) ${\log _3}(\frac{x^2+ x + 3}{2x^2+ 4x + 5}) = x^2+ 3x + 2$
Bài tập 1.3. Giải các phương trình sau:
$\quad \quad $ a) ${3^x} + {4^x} + {5^x}$
$\quad \quad $ b) ${9^x} + 2(x - 2){3^x} + 2x - 5 = 0$
Vấn đề 2. Ứng dụng tính đơn điệu của hàm số để giải bất phương trình, hệ phương trình
Ví dụ 2.1. Giải các bất phương trình sau:
$\quad$ a) $\sqrt {x + 5} + \sqrt {2x + 3} < 9$
$\quad$ b) $3\sqrt {3 - 2x} + \frac{5}{{\sqrt {2x - 1} }} - 2x \leqslant 6$
$\quad$ c) $\sqrt {{x^2} - 2x + 3} - \sqrt {{x^2} - 6x + 11} > \sqrt {3 - x} - \sqrt {x - 1} $
$\quad$ Nhận định: Câu 1, bạn hoàn toàn có thể sử dụng phương pháp bình phương hoặc biến đổi tương đương để giải. Tuy nhiên, tôi muốn hướng bạn đến việc sử dụng tính đơn điệu của hàm số để giải quyết, tuy nhiên đoán được một nghiệm của phương trình này mất khá nhiều thời gian (bạn chú ý chọn những số sao cho biểu thức dưới dấu căn là số chính phương).
Câu 2, có thể đặt ẩn phụ, nhưng biến đổi khá rối. Bài toán đơn giản nếu sử dụng tính đơn điệu của hàm số.
Câu 3, khá phức tạp và cũng có thể đặt ẩn phụ. Song nếu quan sát kỹ thì thấy có mối quan hệ tương tự như Ví dụ 1.2.
Lời giải.
a) Điều kiện: $x \geqslant -\frac{3}{2}$
Bất phương trình đã cho tương đương với $\sqrt {x+5}+ \sqrt {2x+3}-9<0$
Xét hàm số $f(x): = \sqrt {x + 5} + \sqrt {2x + 3}-9$ trên $[- \frac{3}{2};+ \infty)$.
Ta có hàm số $f(x)$ là hàm số liên tục và có đạo hàm $f'(x) = \frac{1}{2\sqrt {x + 5}} + \frac{1}{\sqrt {2x + 3}} > 0,\forall x \in (- \frac{3}{2}: + \infty)$ nên $f(x)$ đồng biến trên $(- \frac{3}{2}: + \infty)$.
Hơn nữa $f(11) = \sqrt {16} + \sqrt {25}- 9 = 0$.
Do đó, miền nghiệm của bất phương trình đã cho phải thỏa mãn:
$$\left\{ \begin{gathered}
x \geqslant - \frac{3}{2} \\
f\left( x \right) < f\left( {11} \right) \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \geqslant - \frac{3}{2} \\
x < 11 \\
\end{gathered} \right.$$
Kết luận: Tập nghiệm của bất phương trình là: $S= [- \frac{3}{2};11)$.
b) Điều kiện: $\frac{1}{2} < x \leqslant \frac{3}{2}$
Đặt $f\left( x \right): = 3\sqrt {3 - 2x} + \frac{5}{{\sqrt {2x - 1} }} - 2x$.
Khi đó $f(x)$ liên tục trên $( {\frac{1}{2};\frac{3}{2}}]$ và có đạo hàm $f'(x) = - \frac{3}{{\sqrt {3 - 2x} }} - \frac{5}{\sqrt {2x - 1}} - 2 < 0,\forall x \in (\frac{1}{2};\frac{3}{2})$ nên nó nghịch biến trên $(\frac{1}{2};\frac{3}{2})$.
Hơn nữa $f(1)=6$.
Do đó, tập nghiệm của phương trình phải thỏa mãn: $\left\{ \begin{gathered}
\frac{1}{2} < x \leqslant \frac{3}{2} \\
x \geqslant 1 \\
\end{gathered} \right. \Leftrightarrow 1 \leqslant x \leqslant \frac{3}{2}$
Kết luận: Tập nghiệm của bất phương trình là: $S = [1;\frac{3}{2}]$
c) Điều kiện: $1 \leqslant x \leqslant 3$
Bất phương trình đã cho tương đương: $$\sqrt {{x^2} - 2x + 3} + \sqrt {x - 1} > \sqrt {x^2 - 6x + 11} + \sqrt {3 - x} $$
$$ \Leftrightarrow \sqrt {(x-1)^2+ 2}+ \sqrt {x - 1} > \sqrt {(3- x)^2+2}+ \sqrt {3 - x} \quad \quad (1)$$
Đặt $u: = (x - 1)^2$ và $v: = (3 - x)^2$ thì (1) thành $\sqrt {u + 2} + \sqrt u > \sqrt {v + 2} + \sqrt v $ hay $f(u)>f(v)$.
Xét hàm số $f(t) = \sqrt {t+2}+ \sqrt t $ trên $[1;3]$.
Khi đó $f(x)$ là hàm liên tục trên $[1;3]$ và có đạo hàm $f'(x) = \frac{1}{2\sqrt {x + 2}} + \frac{1}{2\sqrt x }>0$ trên $[1;3]$ nên hàm $f(t)$ đồng biến trên $[1;3]$.
Vì tính đồng biến nên từ $f(u)>f(v)$ suy ra $u>v$ hay $x-1>3-x \Leftrightarrow x>2$.
Kết hợp với điều kiện ta có: $2 < x \leqslant 3$
Kết luận: Tập hợp nghiệm của bất phương trình là: $S=(2;3]$.
Ví dụ 2.1. Giải các bất phương trình sau:
$\quad$ a) $\sqrt {x + 5} + \sqrt {2x + 3} < 9$
$\quad$ b) $3\sqrt {3 - 2x} + \frac{5}{{\sqrt {2x - 1} }} - 2x \leqslant 6$
$\quad$ c) $\sqrt {{x^2} - 2x + 3} - \sqrt {{x^2} - 6x + 11} > \sqrt {3 - x} - \sqrt {x - 1} $
$\quad$ Nhận định: Câu 1, bạn hoàn toàn có thể sử dụng phương pháp bình phương hoặc biến đổi tương đương để giải. Tuy nhiên, tôi muốn hướng bạn đến việc sử dụng tính đơn điệu của hàm số để giải quyết, tuy nhiên đoán được một nghiệm của phương trình này mất khá nhiều thời gian (bạn chú ý chọn những số sao cho biểu thức dưới dấu căn là số chính phương).
Câu 2, có thể đặt ẩn phụ, nhưng biến đổi khá rối. Bài toán đơn giản nếu sử dụng tính đơn điệu của hàm số.
Câu 3, khá phức tạp và cũng có thể đặt ẩn phụ. Song nếu quan sát kỹ thì thấy có mối quan hệ tương tự như Ví dụ 1.2.
Lời giải.
a) Điều kiện: $x \geqslant -\frac{3}{2}$
Bất phương trình đã cho tương đương với $\sqrt {x+5}+ \sqrt {2x+3}-9<0$
Xét hàm số $f(x): = \sqrt {x + 5} + \sqrt {2x + 3}-9$ trên $[- \frac{3}{2};+ \infty)$.
Ta có hàm số $f(x)$ là hàm số liên tục và có đạo hàm $f'(x) = \frac{1}{2\sqrt {x + 5}} + \frac{1}{\sqrt {2x + 3}} > 0,\forall x \in (- \frac{3}{2}: + \infty)$ nên $f(x)$ đồng biến trên $(- \frac{3}{2}: + \infty)$.
Hơn nữa $f(11) = \sqrt {16} + \sqrt {25}- 9 = 0$.
Do đó, miền nghiệm của bất phương trình đã cho phải thỏa mãn:
$$\left\{ \begin{gathered}
x \geqslant - \frac{3}{2} \\
f\left( x \right) < f\left( {11} \right) \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \geqslant - \frac{3}{2} \\
x < 11 \\
\end{gathered} \right.$$
Kết luận: Tập nghiệm của bất phương trình là: $S= [- \frac{3}{2};11)$.
b) Điều kiện: $\frac{1}{2} < x \leqslant \frac{3}{2}$
Đặt $f\left( x \right): = 3\sqrt {3 - 2x} + \frac{5}{{\sqrt {2x - 1} }} - 2x$.
Khi đó $f(x)$ liên tục trên $( {\frac{1}{2};\frac{3}{2}}]$ và có đạo hàm $f'(x) = - \frac{3}{{\sqrt {3 - 2x} }} - \frac{5}{\sqrt {2x - 1}} - 2 < 0,\forall x \in (\frac{1}{2};\frac{3}{2})$ nên nó nghịch biến trên $(\frac{1}{2};\frac{3}{2})$.
Hơn nữa $f(1)=6$.
Do đó, tập nghiệm của phương trình phải thỏa mãn: $\left\{ \begin{gathered}
\frac{1}{2} < x \leqslant \frac{3}{2} \\
x \geqslant 1 \\
\end{gathered} \right. \Leftrightarrow 1 \leqslant x \leqslant \frac{3}{2}$
Kết luận: Tập nghiệm của bất phương trình là: $S = [1;\frac{3}{2}]$
c) Điều kiện: $1 \leqslant x \leqslant 3$
Bất phương trình đã cho tương đương: $$\sqrt {{x^2} - 2x + 3} + \sqrt {x - 1} > \sqrt {x^2 - 6x + 11} + \sqrt {3 - x} $$
$$ \Leftrightarrow \sqrt {(x-1)^2+ 2}+ \sqrt {x - 1} > \sqrt {(3- x)^2+2}+ \sqrt {3 - x} \quad \quad (1)$$
Đặt $u: = (x - 1)^2$ và $v: = (3 - x)^2$ thì (1) thành $\sqrt {u + 2} + \sqrt u > \sqrt {v + 2} + \sqrt v $ hay $f(u)>f(v)$.
Xét hàm số $f(t) = \sqrt {t+2}+ \sqrt t $ trên $[1;3]$.
Khi đó $f(x)$ là hàm liên tục trên $[1;3]$ và có đạo hàm $f'(x) = \frac{1}{2\sqrt {x + 2}} + \frac{1}{2\sqrt x }>0$ trên $[1;3]$ nên hàm $f(t)$ đồng biến trên $[1;3]$.
Vì tính đồng biến nên từ $f(u)>f(v)$ suy ra $u>v$ hay $x-1>3-x \Leftrightarrow x>2$.
Kết hợp với điều kiện ta có: $2 < x \leqslant 3$
Kết luận: Tập hợp nghiệm của bất phương trình là: $S=(2;3]$.
Bài tập 2.1. Giải các bất phương trình sau:
$\quad$ a) $\sqrt {x + 9} + \sqrt {2x + 4} > 5$
$\quad$ b) $\sqrt {2{x^3} + 3{x^2} + 6x + 16} < \sqrt {4 - x} + 2\sqrt 3 $
$\quad$ c) $\sqrt {x + 1} + \root 3 \of {5x - 7} + \root 4 \of {7x - 5} + \root 5 \of {13x - 7} < 8$
$\quad$ d) ${\log _7}x > {\log _3}\left( {2 + \sqrt x } \right)$
Ví dụ 2.2. Giải các hệ phương trình sau:
$\quad$ $\quad$ a) $\left\{ \begin{gathered}
\cot x - \cot y = x - y \\
5x + 8y = 2\pi \\
x,y \in \left( {0;\pi } \right) \\
\end{gathered} \right.$
$\quad$ $\quad$b) $\left\{ \begin{gathered}
x = {y^3} + {y^2} + y - 2 \\
y = {z^3} + {z^2} + z - 2 \\
z = {x^3} + {x^2} + x - 2 \\
\end{gathered} \right.$
$\quad$ Nhận định: Hệ thứ nhất biến đổi và chọn xét một hàm số đặc trưng.
Hệ thứ hai có dạng hoán vị vòng quanh:
$$\left\{ \begin{gathered}
f\left( {{x_1}} \right) = g\left( {{x_2}} \right) \\
f\left( {{x_2}} \right) = g\left( {{x_3}} \right) \\
... \\
f\left( {{x_n}} \right) = g\left( {{x_1}} \right) \\
\end{gathered} \right.$$
$\quad$ Giả sử $f$ và $g$ cùng đồng biến (hoặc cùng nghịch biến) trên miền $D$ thì khi đó, nếu $(x_1,x_2,...,x_n)$ là nghiệm thì $x_1 = x_2 = ... = x_n$.
Lời giải.
a) Ta có $\cot x - \cot y = x - y \Leftrightarrow x - \cot x = y - \cot y \quad \quad (1)$
Xét hàm số $f(t) = t - \cot t$ với $t \in (0;\pi)$.
Khi đó $f(t)$ là hàm sơ cấp nên liên tục trên TXĐ của nó, hơn nữa đạo hàm $f'(t) = 1 + \frac{1}{{\sin }^2t} > 0,\forall t \in (0;\pi)$ nên $f(t)$ tăng trên $(0;\pi)$
Do đó $(1) \Leftrightarrow f(x) = f(y) \Leftrightarrow x = y$
Hệ đã cho tương đương với hệ: $$\left\{ \begin{gathered}
x = y \\
5x + 8y = 2\pi \\
x,y \in \left( {0;\pi } \right) \\
\end{gathered} \right. \Leftrightarrow x = y = \frac{{2\pi }}{{13}}$$
Kết luận: Hệ có nghiệm duy nhất: $\boxed{x = y = \frac{{2\pi }}{{13}}}$
b) Xét hàm số đặc trưng $f(t) = {t^3} + {t^2} + t - 2$.
Khi đó hệ đã cho trở thành: $\left\{ \begin{gathered}
x= f(y) \\
y= f(z)\\
z= f(x) \\
\end{gathered} \right.\quad \quad (*)$
Và có: $f'(t) = 3{t^2} + 2t + 1 > 0$ với mọi $\forall t \in \mathbb{R}$
Vậy $f(t)$ là hàm số đồng biến trên $\mathbb R$
(Chứng minh tính chất 5 bắt đầu từ đoạn này!)
Giải sử $(x,y,z)$ là một nghiệm của hệ vậy thì chúng phải thỏa mãn hệ (*)!
Không mất tính tổng quát ta có thể giả sử $x \leqslant y \leqslant z$.
\begin{align*}
& \Rightarrow f(x) \leqslant f(y) \leqslant f(z) \quad \quad \text{(vì f là hàm tăng trên } \mathbb R)\\
& \Rightarrow z \leqslant x \leqslant y \quad \quad \text{(do (*))}
\end{align*}
Vậy $\left\{ \begin{gathered}
x \leqslant y \leqslant z \\
z \leqslant x \leqslant y \\
\end{gathered} \right. \Leftrightarrow x = y = z$.
(Kết thúc chứng minh tính chất 5)
Thay vào hệ đã cho, ta có:
$${x^3} + {x^2} - 2 = 0 \Leftrightarrow (x - 1)({x^2} + 2x + 2) = 0 \Leftrightarrow x = 1$$
Kết luận: Hệ có nghiệm duy nhất là: $x=y=z=1$
Chú ý: Khi thay $x=y=z$ trở lại hệ ta thu được một phương trình bậc 3 với ẩn $x$ và việc giải phương trình đó khá dễ dàng. Tuy nhiên, khi giải phương trình này gặp khó khăn thì các bạn nhớ đặt hàm, khảo sát, đoán nghiệm và khẳng định phương trình có nghiệm duy nhất như đã trình bày ở Vấn đề 1.
Các bạn có thể xem Bài tập 2.2 câu d)!
Bài tập 2.2. Giải các hệ phương trình sau:
$\quad$ a) $\left\{ \begin{gathered}
\cot x - \cot y = x - y \\
3x + 5y = 2\pi \\
x,y \in \left( {0;\pi } \right) \\
\end{gathered} \right.$
$\quad$ b) $\left\{ \begin{gathered}
x - y = \sin x - \sin y \\
\sin x + \sin y = \sqrt 2 \\
\end{gathered} \right.$
$\quad$ c) $\left\{ \begin{gathered}
{\log _5}x = {\log _3}(\sqrt y + 4) \\
{\log _5}y = {\log _3}(\sqrt z + 4) \\
{\log _5}z = {\log _3}(\sqrt x + 4) \\
\end{gathered} \right.$
$\quad$ d) $\left\{ \begin{gathered}
{x^3} + 3x - 3 + \ln \left( {{x^2} - x + 1} \right) = y \\
{y^3} + 3y - 3 + \ln \left( {{y^2} - y + 1} \right) = z \\
{z^3} + 3z - 3 + \ln \left( {{z^2} - z + 1} \right) = x \\
\end{gathered} \right.$
$\quad$ e) (D-2006). Chứng minh rằng với mọi $a>0$ hệ phương trình sau có nghiệm duy nhất
\[\left\{ \begin{gathered}
{e^x} - {e^y} = \ln \left( {1 + x} \right) - \ln \left( {1 + y} \right) \\
y - x = a \\
\end{gathered} \right.\]
Vấn đề 3. Ứng dụng tính đơn điệu của hàm số để chứng minh bất đẳng thức
I.TÓM TẮT LÝ THUYẾT:
Như các bạn đã biết ,tính đơn điệu của hàm số phụ thuộc vào đạo hàm của hàm số đó.Dùng đạo hàm,ta có thể xét được tính đồng biến và nghịch biến của 1 hàm số trên 1 miền nào đó,do đó chúng có thể ứng dụng để chứng minh khá nhiều Bất đẳng thức(BĐT).Ta xét phương pháp cụ thể như sau:
Xét hàm số $f(x)$ trên đoạn $[a;b]$.
* Nếu $f'(x) \ge 0;\forall x \in [a;b] \iff$ hàm số $f(x)$ đồng biến trên $[a;b]$.Suy ra:$f(b) \ge f(x) \ge f(a)$
* Nếu $f'(x) \ge 0;\forall x \in [a;b] \iff$ hàm số $f(x)$ nghịch biến trên $[a;b]$.Suy ra:$f(b) \le f(x) \le f(a)$
Lưu ý: Khi ta sử dụng điều kiện $f'(x) \ge 0;\forall x \in [a;b]$ hay $f'(x) \le 0;\forall x \in [a;b]$ thì ta phải đảm bảo phương trình $f'(x)=0$ chỉ xảy ra tại hữu hạn điểm,tức là phương trình này chỉ có hữu hạn nghiệm mà thôi.Lưu ý trên đặc biệt quan trọng khi ta xét đến các hàm số lượng giác.Điều này cũng dễ hiểu bởi khi ta đề cập đến “nghiệm” của 1 phương trình lượng giác,ta chỉ sử dụng khái niệm “tập nghiệm” để biểu diễn các giá trị thỏa mãn phương trình lượng giác cho trước.Nói một cách nôm na,phương trình lượng giác luôn có vô hạn nghiệm.Do đó khi ta muốn chứng minh các BĐT liên quan đến các hàm lượng giác phức tạp,ta phải sử dụng đến phương pháp đại số hóa,vấn đề đó sẽ được trình bày trong chuyên đề lượng giác.
Như các bạn đã biết ,tính đơn điệu của hàm số phụ thuộc vào đạo hàm của hàm số đó.Dùng đạo hàm,ta có thể xét được tính đồng biến và nghịch biến của 1 hàm số trên 1 miền nào đó,do đó chúng có thể ứng dụng để chứng minh khá nhiều Bất đẳng thức(BĐT).Ta xét phương pháp cụ thể như sau:
Xét hàm số $f(x)$ trên đoạn $[a;b]$.
* Nếu $f'(x) \ge 0;\forall x \in [a;b] \iff$ hàm số $f(x)$ đồng biến trên $[a;b]$.Suy ra:$f(b) \ge f(x) \ge f(a)$
* Nếu $f'(x) \ge 0;\forall x \in [a;b] \iff$ hàm số $f(x)$ nghịch biến trên $[a;b]$.Suy ra:$f(b) \le f(x) \le f(a)$
Lưu ý: Khi ta sử dụng điều kiện $f'(x) \ge 0;\forall x \in [a;b]$ hay $f'(x) \le 0;\forall x \in [a;b]$ thì ta phải đảm bảo phương trình $f'(x)=0$ chỉ xảy ra tại hữu hạn điểm,tức là phương trình này chỉ có hữu hạn nghiệm mà thôi.Lưu ý trên đặc biệt quan trọng khi ta xét đến các hàm số lượng giác.Điều này cũng dễ hiểu bởi khi ta đề cập đến “nghiệm” của 1 phương trình lượng giác,ta chỉ sử dụng khái niệm “tập nghiệm” để biểu diễn các giá trị thỏa mãn phương trình lượng giác cho trước.Nói một cách nôm na,phương trình lượng giác luôn có vô hạn nghiệm.Do đó khi ta muốn chứng minh các BĐT liên quan đến các hàm lượng giác phức tạp,ta phải sử dụng đến phương pháp đại số hóa,vấn đề đó sẽ được trình bày trong chuyên đề lượng giác.
II.VÍ DỤ VÀ BÀI TẬP:
Ví dụ 3.1: Cho $0<x<\frac{\pi}{2}$. ch="" ng="" minh="" span="">
1. $\sin{x}<x$
2. $\tan{x}>x$
Ví dụ 3.1: Cho $0<x<\frac{\pi}{2}$. ch="" ng="" minh="" span="">
1. $\sin{x}<x$
2. $\tan{x}>x$
Định hướng giải: Với các hàm số đơn giản như ví dụ trên thì ta nên đưa BĐT về dạng $f(x)>0$ hay $f(x)
Lời giải:
Xét hàm số $f(x)=\sin{x}-x \left(0 < x < \frac{\pi}{2} \right)$
Đạo hàm: $f'(x)=\cos{x}-1<0;\forall x="" in="" left="" 0="" frac="" pi="" 2="" right="" span="">
Xét hàm số $f(x)=\sin{x}-x \left(0 < x < \frac{\pi}{2} \right)$
Đạo hàm: $f'(x)=\cos{x}-1<0;\forall x="" in="" left="" 0="" frac="" pi="" 2="" right="" span="">
Hàm số $f(x)$ nghịch biến trên $\left(0;\frac{\pi}{2} \right)$. Nên:
$$f(x)
Bài dưới làm tương tự.
Lưu ý: Đôi khi ta không thể kết luận ngay được $f'(x) \ge 0;\forall x \in [a;b]$ hay $f'(x) \le 0;\forall x \in [a;b]$,ví dụ như hàm số:$f(x)=x-\frac{x^3}{6}-\sin{x}(x>0)$ ta có
$f'(x)=1-\frac{x^2}{2}-\cos{x}$,rõ ràng là ta không thể xác định được dấu của $f'(x)$ trên khoảng $(0;+\infty)$.Khi ta gặp phải các dạng bài như thế này,ta phải sử dụng thủ thuật lien tiếp đạo hàm để hạ bậc dần dần của hàm số ẩn x.Ta sẽ xem xét điều này trong ví dụ sau đây:
$f'(x)=1-\frac{x^2}{2}-\cos{x}$,rõ ràng là ta không thể xác định được dấu của $f'(x)$ trên khoảng $(0;+\infty)$.Khi ta gặp phải các dạng bài như thế này,ta phải sử dụng thủ thuật lien tiếp đạo hàm để hạ bậc dần dần của hàm số ẩn x.Ta sẽ xem xét điều này trong ví dụ sau đây:
Ví dụ 3.2: Chứng minh rằng:$x-\frac{x^3}{6}0$
Lời giải:
Xét hàm số $f(x)=x-\frac{x^3}{6}-\sin{x}(x>0)$
Đạo hàm:
Lời giải:
Xét hàm số $f(x)=x-\frac{x^3}{6}-\sin{x}(x>0)$
Đạo hàm:
$$f'(x)=1-\frac{x^2}{2}-\cos{x}; f''(x)=\sin{x}-x$$.
Ta đã chứng minh trong ví dụ 1 BĐT:$\sin{x}0$ nên ta có $f''(x)0 \iff f'(x)$ nghịch biến trên $(0;+\infty)$.Suy ra:
$f'(x)0 \iff f(x)$ nghịch biến trên $(0;+\infty)$.
Suy ra:
$f'(x)0 \iff f(x)$ nghịch biến trên $(0;+\infty)$.
Suy ra:
$$f(x)0 \iff x-\frac{x^3}{6}0$$
Nếu bạn nào đã từng tìm hiểu sâu về BĐT này thì có thể thấy ngay nó chỉ là hệ quả của định nghĩa chuỗi cho $\sin{x}$:
$$\sin{x}=\sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n+1}}{(2n+1)!}$$
Ví dụ 3.3: Chứng minh rằng trong mọi tam giác nhọn ABC ta đều có:
$$2(\sin{A}+\sin{B}+\sin{C})+(\tan{A}+\tan{B}+\tan{C})>3\pi$$
Định hướng giải: Ta phải để ý đến giả thuyết $A,B,C$ là 3 góc tam giác nên ta có thể thay $\pi=A+B+C$,như vậy cả 2 vế của BĐT đều xuất hiện các số hạng chứa A,B,C, nên ta có thể nhóm BĐT về dạng sau:$f(A)+f(B)+f\left(C \right)>0$ với
$f(A)=2\sin{A}+\tan{A}-3A$. Ta sẽ chứng minh:$f(A);f(B);f\left(C \right)>0$.
$f(A)=2\sin{A}+\tan{A}-3A$. Ta sẽ chứng minh:$f(A);f(B);f\left(C \right)>0$.
Lời giải: Do tam giác ABC nhọn nên $0<A,B,C<\frac{\pi}{2}$.
Xét hàm số $f(x)=2\sin{x}+\tan{x}-3x \left(0<x
Đạo hàm:
$$f'(x)=2\cos{x}+\frac{1}{\cos^2{x}}-3=\left(\cos{x}+\cos{x}+\frac{1}{\cos^2{x}} \right)-3$$.
Do $0
Xét hàm số $f(x)=2\sin{x}+\tan{x}-3x \left(0<x
Đạo hàm:
$$f'(x)=2\cos{x}+\frac{1}{\cos^2{x}}-3=\left(\cos{x}+\cos{x}+\frac{1}{\cos^2{x}} \right)-3$$.
Do $0
$$\cos{x}+\cos{x}+\frac{1}{\cos^2{x}} \ge 3\sqrt[3]{\cos{x}.\cos{x}.\frac{1}{\cos^2{x}}}=3$$
Vậy :$f'(x) \ge 0;\forall x\ in \left(0;\frac{\pi}{2} \right) \iff f(x)$ đồng biến trên $\left(0;\frac{\pi}{2} \right)$
Vậy :$f'(x) \ge 0;\forall x\ in \left(0;\frac{\pi}{2} \right) \iff f(x)$ đồng biến trên $\left(0;\frac{\pi}{2} \right)$
$$f(x)>f(0)=0 \iff 2\sin{x}+\tan{x}>3x;\forall x \in \left(0;\frac{\pi}{2} \right)$$
.Như vậy:
.Như vậy:
$$2(\sin{A}+\sin{B}+\sin{C})+(\tan{A}+\tan{B}+\tan{C})>3(A+B+C)=3\pi$$
Lưu ý: Trong lời giải trên,để chứng minh $f'(x) \ge 0;\forall x \in \left(0;\frac{\pi}{2} \right)$ ,ta đã sử dụng đến BĐT Cauchy 3 số.Như vậy,ta có thể thấy không phải lúc nào ta cũng chỉ có thể dựa vào tính đơn điệu của hàm số để chứng minh BĐT mà còn phải dựa trên các BĐT khác như :BĐT Cauchy;BĐT BCS;….Ta đi đến 1 ví dụ minh họa:
Ví dụ 3.4: Chứng minh rằng với $0<x2^{\frac{3x}{2}+1}$
Định hướng giải: Nếu ta trực tiếp khảo sát hàm số $f(x)=2^{2\sin{x}}+2^{\tan{x}}-2^{\frac{3x}{2}+1}\left(0<x<\frac{\pi}{2} right="" span="">
Thì ta không thể nào nhận xét được dấu của $f'(x)$,hon nua ta áp dụng thủ thuật đạo hàm lien tiếp thì cũng không giúp ta đi đến đâu.Vậy ta phải làm sao ?
Bây giờ ta để ý thấy rằng các số hạng của 2 vế BĐT đều có chung 1 cơ số 2,do đó ta sẽ nghĩ ngay đến đưa BĐT này về dạng bất phương trình mũ.Nhưng phải làm sao để có thể gộp 2 số mũ $2\sin{x};\tan{x}$ lại với nhau ? Ta nhớ đến công thức :
$a^{m}.a^{n}=a^{m+n}(a>0)$.Như vậy chỉ cần ta có thể “biến” tổng 2 số hạng bên vế trái(VT) của BĐT về dạng tích thì ta đã có thể giải quyết bài toán,ta phải làm gì để giải quyết điều này ?May thay BĐT Cauchy sẽ giúp ta vượt qua vấn đề đó.
Bây giờ ta để ý thấy rằng các số hạng của 2 vế BĐT đều có chung 1 cơ số 2,do đó ta sẽ nghĩ ngay đến đưa BĐT này về dạng bất phương trình mũ.Nhưng phải làm sao để có thể gộp 2 số mũ $2\sin{x};\tan{x}$ lại với nhau ? Ta nhớ đến công thức :
$a^{m}.a^{n}=a^{m+n}(a>0)$.Như vậy chỉ cần ta có thể “biến” tổng 2 số hạng bên vế trái(VT) của BĐT về dạng tích thì ta đã có thể giải quyết bài toán,ta phải làm gì để giải quyết điều này ?May thay BĐT Cauchy sẽ giúp ta vượt qua vấn đề đó.
Lời giải:
Sử dụng BĐT Cauchy 2 số,ta có:
Sử dụng BĐT Cauchy 2 số,ta có:
$$2^{2\sin{x}}+2^{\tan{x}} \ge 2\sqrt{2^{2\sin{x}}.2^{\tan{x}}}=2^{\frac{2\sin{x}+\tan{x}}{2}+1}$$
Như vậy ta chỉ cần chứng minh:
Như vậy ta chỉ cần chứng minh:
$$2^{\frac{2\sin{x}+\tan{x}}{2}+1}>2^{\frac{3x}{2}+1} \iff 2\sin{x}+\tan{x}>3x$$
BĐT này đã được chứng minh trong ví dụ 3 nên ta giải quyết xong bài toán.
BĐT này đã được chứng minh trong ví dụ 3 nên ta giải quyết xong bài toán.
Ví dụ 3.5. Chứng minh rằng: $1 + 2\ln x \leqslant {x^2} \quad \quad$ (1), với mọi $x>0$
Lời giải. (1) $ \Leftrightarrow {x^2} - 2\ln x - 1 \geqslant 0$.
Đặt $f(x): =x^2- 2\ln x - 1$, ta sẽ chứng minh hàm số $f(x) \geqslant 0$, với $x \in (0; + \infty)$
Ta có: $f(x)$ là hàm liên tục trên $(0; + \infty)$ và
$$f'(x) &= 2x - \frac{2}{x} = \frac{2(x^2- 1)}{x}$$
$f'(x) = 0 \Leftrightarrow x = 1$ trên $(0; + \infty)$.
Lập bảng biến thiên của hàm $f$ trên $(0; + \infty)$ như sau:
Lời giải. (1) $ \Leftrightarrow {x^2} - 2\ln x - 1 \geqslant 0$.
Đặt $f(x): =x^2- 2\ln x - 1$, ta sẽ chứng minh hàm số $f(x) \geqslant 0$, với $x \in (0; + \infty)$
Ta có: $f(x)$ là hàm liên tục trên $(0; + \infty)$ và
$$f'(x) &= 2x - \frac{2}{x} = \frac{2(x^2- 1)}{x}$$
$f'(x) = 0 \Leftrightarrow x = 1$ trên $(0; + \infty)$.
Lập bảng biến thiên của hàm $f$ trên $(0; + \infty)$ như sau:
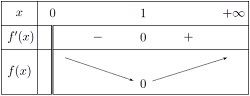
Từ bảng biến thiên suy ra $f(x) \geqslant 0,\forall x > 0.\quad \quad \square $
Ví dụ 3.6. Chứng minh rằng với mọi số thực $x>1$, ta đều có:
$$\frac{{\ln x}}{{x - 1}} \leqslant \frac{1}{{\sqrt x }} \quad \quad (1)$$
Lời giải. Với $x>1$, bất đẳng thức (1) tương đương với:
$$\ln x \leqslant \frac{x - 1}{\sqrt x } \Leftrightarrow \ln x - \frac{x - 1}{\sqrt x } \leqslant 0$$
Xét hàm số $f(x) = \ln x - \frac{x - 1}{\sqrt x } = \ln x - (x - 1){x^{ - \frac{1}{2}}}$ trên $[1; + \infty)$
Ta thấy hàm $f(x)$ liên tục trên $[1; + \infty)$ và có:
$$f'(x) &= \frac{1}{x} - x^{ - \frac{1}{2}} + \frac{1}{2}(x - 1){x^{ - \frac{3}{2}}}= \frac{2\sqrt x - x - 1}{2x\sqrt x }: = \frac{g(x)}{2x\sqrt x }$$
Dấu của $f'(x)$ là dấu của $g(x)$ với $g(x)=2\sqrt x - x - 1$, với $x \geqslant 1$
Hàm số $g(x)$ liên tục trên $[1; + \infty)$ và có $g'(x) = \frac{1}{\sqrt x } - 1 1$.
Do đó hàm $g(x)$ nghịch biến trên $[1; + \infty)$ và $g(1)=0$ suy ra $g( x) < g(1) = 0$
Từ đó ta có $f'(x)1$ nên hàm số $f(x)$ nghịch biến trên $[1; + \infty)$ và
$$f(x)1$$
Vậy: $\ln x \leqslant \frac{x - 1}{\sqrt x }.\quad \quad \square$
$$\frac{{\ln x}}{{x - 1}} \leqslant \frac{1}{{\sqrt x }} \quad \quad (1)$$
Lời giải. Với $x>1$, bất đẳng thức (1) tương đương với:
$$\ln x \leqslant \frac{x - 1}{\sqrt x } \Leftrightarrow \ln x - \frac{x - 1}{\sqrt x } \leqslant 0$$
Xét hàm số $f(x) = \ln x - \frac{x - 1}{\sqrt x } = \ln x - (x - 1){x^{ - \frac{1}{2}}}$ trên $[1; + \infty)$
Ta thấy hàm $f(x)$ liên tục trên $[1; + \infty)$ và có:
$$f'(x) &= \frac{1}{x} - x^{ - \frac{1}{2}} + \frac{1}{2}(x - 1){x^{ - \frac{3}{2}}}= \frac{2\sqrt x - x - 1}{2x\sqrt x }: = \frac{g(x)}{2x\sqrt x }$$
Dấu của $f'(x)$ là dấu của $g(x)$ với $g(x)=2\sqrt x - x - 1$, với $x \geqslant 1$
Hàm số $g(x)$ liên tục trên $[1; + \infty)$ và có $g'(x) = \frac{1}{\sqrt x } - 1 1$.
Do đó hàm $g(x)$ nghịch biến trên $[1; + \infty)$ và $g(1)=0$ suy ra $g( x) < g(1) = 0$
Từ đó ta có $f'(x)1$ nên hàm số $f(x)$ nghịch biến trên $[1; + \infty)$ và
$$f(x)1$$
Vậy: $\ln x \leqslant \frac{x - 1}{\sqrt x }.\quad \quad \square$
Ví dụ 3.7. Chứng minh rằng với mọi $a, b \in \mathbb{R}$, ta đều có:
$$\frac{{\left| {a + b} \right|}}{{1 + \left| {a + b} \right|}} \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}}$$
Lời giải. Xét hàm số $f(x) = \frac{x}{1 + x}$ trên khoảng $[0;+ \infty)$
Ta có $f'(x) = \frac{1}{(1 + x)^2} > 0$ với mọi $x \geqslant 0$
Do đó hàm số $f$ đồng biến trên khoảng $[0; + \infty)$
Từ đó suy ra $f(|a + b|) \leqslant f(|a| +|b|)$ với mọi $a,b \in \mathbb{R}$
tức là $\frac{|a+b|}{1+|a+b|} \leqslant \frac{|a|+|b|}{1+|a|+| b |}$ với mọi $a,b \in \mathbb{R} \quad (1)$
Mặt khác ta có
\begin{align*}
\frac{{\left| a \right| + \left| b \right|}}{{1 + \left| a \right| + \left| b \right|}} &= \frac{{\left| a \right|}}{{1 + \left| a \right| + \left| b \right|}} + \frac{{\left| b \right|}}{{1 + \left| a \right| + \left| b \right|}}\\
& \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}} \quad (2)
\end{align*}
Từ (1) và (2) ta có
$$\frac{{\left| {a + b} \right|}}{{1 + \left| {a + b} \right|}} \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}} \quad \square$$
$$\frac{{\left| {a + b} \right|}}{{1 + \left| {a + b} \right|}} \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}}$$
Lời giải. Xét hàm số $f(x) = \frac{x}{1 + x}$ trên khoảng $[0;+ \infty)$
Ta có $f'(x) = \frac{1}{(1 + x)^2} > 0$ với mọi $x \geqslant 0$
Do đó hàm số $f$ đồng biến trên khoảng $[0; + \infty)$
Từ đó suy ra $f(|a + b|) \leqslant f(|a| +|b|)$ với mọi $a,b \in \mathbb{R}$
tức là $\frac{|a+b|}{1+|a+b|} \leqslant \frac{|a|+|b|}{1+|a|+| b |}$ với mọi $a,b \in \mathbb{R} \quad (1)$
Mặt khác ta có
\begin{align*}
\frac{{\left| a \right| + \left| b \right|}}{{1 + \left| a \right| + \left| b \right|}} &= \frac{{\left| a \right|}}{{1 + \left| a \right| + \left| b \right|}} + \frac{{\left| b \right|}}{{1 + \left| a \right| + \left| b \right|}}\\
& \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}} \quad (2)
\end{align*}
Từ (1) và (2) ta có
$$\frac{{\left| {a + b} \right|}}{{1 + \left| {a + b} \right|}} \leqslant \frac{{\left| a \right|}}{{1 + \left| a \right|}} + \frac{{\left| b \right|}}{{1 + \left| b \right|}} \quad \square$$
Ví dụ 3.8. Cho hai số thực $a, b$ sao cho $0<a<b
$$\frac{{\tan b}}{{\tan a}} > \frac{b}{a}$$
Nhận định: Nếu sử dụng tính đơn điệu để giải thì bạn phải xác định cho được hàm số cần xét là hàm nào? Ở đây để ý rằng $a,b \in (0;\frac{\pi }{2})$ cho nên $\tan a, \tan b > 0$ và $a, b>0$, do đó có thể biến đổi bất đẳng thức đã cho để chứng minh bất đẳng thức dạng: $f(b)>f(a)$
Lời giải.
Do $a,b \in (0;\frac{\pi }{2})$ nên $\tan a, \tan b > 0$ và $a, b>0$. Vậy
\[\frac{\tan b}{\tan a} > \frac{b}{a} \Leftrightarrow \frac{\tan b}{b} > \frac{\tan a}{a}\]
Xét hàm số $f(x) = \frac{\tan x}{x}$ thì bài toán trở thành:
"Cho $a,b \in \left( {0;\frac{\pi }{2}} \right)$ sao cho $b>a$. Hãy chứng minh rằng: $f(b)>f(a)$".
Như vậy theo định nghĩa của tính đơn điệu của hàm số ta chỉ cần chứng minh $f$ đồng biến trên $(a;b)$.
Thật vậy, ta có: $$f'(x) = \frac{{x - \sin x\cos x}}{{{x^2}{{\cos }^2}x}} = :\frac{{g(x)}}{{{x^2}{{\cos }^2}x}}$$
Dấu của $f'(x)$ là dấu của hàm $g(x):=x-\sin x \cos x$ trên $[{0;\frac{\pi }{2}}]$. Ta lại có:
$$g(x) = x - \sin x\cos x = x - \frac{\sin x}{2}$$
$$ \Rightarrow g'(x) = 1 - \cos 2x,\forall x \in (0;\frac{\pi }{2})$$
Do đó $g(x)$ đồng biến và $g(x)>g(0)=0, \forall x \in (0;\frac{\pi }{2})$.
Vậy $f'(x)>0, \forall x \in (0;\frac{\pi }{2})$ tức là $f$ đồng biến trên $(0;\frac{\pi }{2})$. $\quad \square $
$$\frac{{\tan b}}{{\tan a}} > \frac{b}{a}$$
Nhận định: Nếu sử dụng tính đơn điệu để giải thì bạn phải xác định cho được hàm số cần xét là hàm nào? Ở đây để ý rằng $a,b \in (0;\frac{\pi }{2})$ cho nên $\tan a, \tan b > 0$ và $a, b>0$, do đó có thể biến đổi bất đẳng thức đã cho để chứng minh bất đẳng thức dạng: $f(b)>f(a)$
Lời giải.
Do $a,b \in (0;\frac{\pi }{2})$ nên $\tan a, \tan b > 0$ và $a, b>0$. Vậy
\[\frac{\tan b}{\tan a} > \frac{b}{a} \Leftrightarrow \frac{\tan b}{b} > \frac{\tan a}{a}\]
Xét hàm số $f(x) = \frac{\tan x}{x}$ thì bài toán trở thành:
"Cho $a,b \in \left( {0;\frac{\pi }{2}} \right)$ sao cho $b>a$. Hãy chứng minh rằng: $f(b)>f(a)$".
Như vậy theo định nghĩa của tính đơn điệu của hàm số ta chỉ cần chứng minh $f$ đồng biến trên $(a;b)$.
Thật vậy, ta có: $$f'(x) = \frac{{x - \sin x\cos x}}{{{x^2}{{\cos }^2}x}} = :\frac{{g(x)}}{{{x^2}{{\cos }^2}x}}$$
Dấu của $f'(x)$ là dấu của hàm $g(x):=x-\sin x \cos x$ trên $[{0;\frac{\pi }{2}}]$. Ta lại có:
$$g(x) = x - \sin x\cos x = x - \frac{\sin x}{2}$$
$$ \Rightarrow g'(x) = 1 - \cos 2x,\forall x \in (0;\frac{\pi }{2})$$
Do đó $g(x)$ đồng biến và $g(x)>g(0)=0, \forall x \in (0;\frac{\pi }{2})$.
Vậy $f'(x)>0, \forall x \in (0;\frac{\pi }{2})$ tức là $f$ đồng biến trên $(0;\frac{\pi }{2})$. $\quad \square $
Ví dụ 3.9. Chứng minh rằng nếu $x \in (0;\frac{\pi }{2})$ thì:
$${2^{\sin x}} + {2^{\tan x}} > {2^{x + 1}}$$
$${2^{\sin x}} + {2^{\tan x}} > {2^{x + 1}}$$
Lời giải.
Do $x \in (0;\frac{\pi }{2})$ nên ${2^{\sin x}}{,2^{\tan x}}$ đều là các số dương. Áp dụng BĐT Cauchy ta có:
$${2^{\sin x}} + {2^{\tan x}} \geqslant 2\sqrt {{2^{\sin x + \tan x}}} $$
$$ \Leftrightarrow {2^{\sin x}} + {2^{\tan x}} \geqslant {2^{\frac{{\sin x + \tan x + 2}}{2}}}$$
Khi đó BĐT đã cho trở thành: ${2^{\frac{{\sin x + \tan x + 2}}{2}}} > {2^{x + 1}}$. Hay
$$\frac{{\sin x + \tan x + 2}}{2} > x + 1 \Leftrightarrow \sin x + \tan x - 2x > 0$$
Đặt và xét hàm số $f\left( x \right) := \sin x + \tan x - 2x > 0$ trên $(0;\frac{\pi }{2})$
Như vậy để chứng minh BĐT đã cho ta chỉ cần chỉ ra rằng: $$f(x) > 0,\forall x \in (0;\frac{\pi }{2})$$
Thật vậy, ta có $$f'(x) = \cos x + \frac{1}{{{\cos }^2}x} - 2$$
Ta sẽ đánh giá sau:
$$f'\left( x \right) = \cos x + \frac{1}{{{{\cos }^2}x}} - 2 > \cos x + \frac{1}{{\cos x}} - 2,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$
Theo BĐT Cauchy thì $$\cos x + \frac{1}{{\cos x}} > 2,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$ bởi vậy $$f'\left( x \right) > 0,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$
Vậy, hàm số $f(x)$ đồng biến trên $(0;\frac{\pi }{2})$
Suy ra với $\forall x \in \left( {0;\frac{\pi }{2}} \right)$ thì $f(x)>f(0)=0$.$\quad \square $
Do $x \in (0;\frac{\pi }{2})$ nên ${2^{\sin x}}{,2^{\tan x}}$ đều là các số dương. Áp dụng BĐT Cauchy ta có:
$${2^{\sin x}} + {2^{\tan x}} \geqslant 2\sqrt {{2^{\sin x + \tan x}}} $$
$$ \Leftrightarrow {2^{\sin x}} + {2^{\tan x}} \geqslant {2^{\frac{{\sin x + \tan x + 2}}{2}}}$$
Khi đó BĐT đã cho trở thành: ${2^{\frac{{\sin x + \tan x + 2}}{2}}} > {2^{x + 1}}$. Hay
$$\frac{{\sin x + \tan x + 2}}{2} > x + 1 \Leftrightarrow \sin x + \tan x - 2x > 0$$
Đặt và xét hàm số $f\left( x \right) := \sin x + \tan x - 2x > 0$ trên $(0;\frac{\pi }{2})$
Như vậy để chứng minh BĐT đã cho ta chỉ cần chỉ ra rằng: $$f(x) > 0,\forall x \in (0;\frac{\pi }{2})$$
Thật vậy, ta có $$f'(x) = \cos x + \frac{1}{{{\cos }^2}x} - 2$$
Ta sẽ đánh giá sau:
$$f'\left( x \right) = \cos x + \frac{1}{{{{\cos }^2}x}} - 2 > \cos x + \frac{1}{{\cos x}} - 2,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$
Theo BĐT Cauchy thì $$\cos x + \frac{1}{{\cos x}} > 2,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$ bởi vậy $$f'\left( x \right) > 0,\forall x \in \left( {0;\frac{\pi }{2}} \right)$$
Vậy, hàm số $f(x)$ đồng biến trên $(0;\frac{\pi }{2})$
Suy ra với $\forall x \in \left( {0;\frac{\pi }{2}} \right)$ thì $f(x)>f(0)=0$.$\quad \square $
Bài tập tự luyện:
Bài tập 3.1. Chứng minh rằng:
$\quad$ a) $x > \ln (1 + x)$ với mọi $x>0$
$\quad$ b) ${e^x} > 1 + \ln (1+x)$ với mọi $x>0$
Bài tập 3.2. Chứng minh:
$$\sin > \frac{{2x}}{\pi } \text{ với mọi } x \in (0;\frac{\pi }{2})$$
Bài tập 3.3. Chứng minh:
$$\frac{x + y}{2} > \frac{x - y}{\ln x - \ln y} \text{ với mọi }x > y > 0$$
Bài tập 3.4. Chứng minh:
$${a^b} b \geqslant e$$
Bài tập 3.5. (D-2007). Chứng minh:
$${({2^a} + \frac{1}{2^a})^b} \leqslant {({2^b} + \frac{1}{{{2^b}}})^a} \text{ với mọi } a \geqslant b > 0$$
Bài tập 3.1. Chứng minh rằng:
$\quad$ a) $x > \ln (1 + x)$ với mọi $x>0$
$\quad$ b) ${e^x} > 1 + \ln (1+x)$ với mọi $x>0$
Bài tập 3.2. Chứng minh:
$$\sin > \frac{{2x}}{\pi } \text{ với mọi } x \in (0;\frac{\pi }{2})$$
Bài tập 3.3. Chứng minh:
$$\frac{x + y}{2} > \frac{x - y}{\ln x - \ln y} \text{ với mọi }x > y > 0$$
Bài tập 3.4. Chứng minh:
$${a^b} b \geqslant e$$
Bài tập 3.5. (D-2007). Chứng minh:
$${({2^a} + \frac{1}{2^a})^b} \leqslant {({2^b} + \frac{1}{{{2^b}}})^a} \text{ với mọi } a \geqslant b > 0$$
Vấn đề 4. Ứng dụng tính đơn điệu để biện luận phương trình và bất phương trình
$\quad$ Bài toán về biện luận số nghiệm, có nghiệm trên một tập hợp cho trước là bài toán mà hầu như trong đề thi năm nào cũng có. Ngoài việc yêu cầu học sinh nắm vững các kiến thức cơ sở, bài toán còn đòi hỏi óc tư duy, sáng tạo. Đối với dạng toán này cũng có nhiều phương án giải quyết, trong đó phương án sử dụng tính đơn điệu của hàm số sẽ cho ta lời giải ngắn gọn, độc đáo và được đánh giá rất cao!
$\quad$ Bài toán về biện luận số nghiệm, có nghiệm trên một tập hợp cho trước là bài toán mà hầu như trong đề thi năm nào cũng có. Ngoài việc yêu cầu học sinh nắm vững các kiến thức cơ sở, bài toán còn đòi hỏi óc tư duy, sáng tạo. Đối với dạng toán này cũng có nhiều phương án giải quyết, trong đó phương án sử dụng tính đơn điệu của hàm số sẽ cho ta lời giải ngắn gọn, độc đáo và được đánh giá rất cao!
Ví dụ 4.1. Cho hàm số $f(x)=mx^2+2mx-3$
$\quad$ a) Tìm $m$ để phương trình: $f(x)=0$ có nghiệm $x \in [1;2]$
$\quad$ b) Tìm $m$ để bất phương trình: $f(x) \leqslant 0$ nghiệm đúng $\forall x \in [1;4]$
$\quad$ c) Tìm $m$ để bất phương trình: $f(x) \geqslant 0$ có nghiệm $x \in [1;3]$
$\quad$ Nhận định: Một cách rất tự nhiên, khi biện luận phương trình hoặc bất phương trình có chứa tham số thì việc đầu tiên cần làm là cố gắng đưa tham số về một vế độc lập. Sau đó sử dụng các tính chất đơn điệu của hàm số mà bạn đã biết. Để tiện đối sánh, tôi xin nhắc lại một số "hằng đẳng thức" sau:
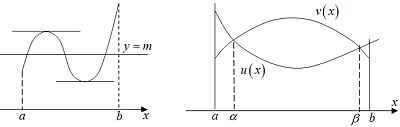
$\quad$ a) Nghiệm của phương trình $u(x)=v(x)$ là hoành độ giao điểm của đồ thị hàm số $y=u(x)$ với đồ thị $y=v(x)$
$\quad$ b) Nghiệm của bất phương trình $u(x) \geqslant v(x)$ là phần hoành độ tương ứng với phần đồ thị $y=u(x)$ nằm ở phía trên so với phần đồ thị $y=v(x)$
$\quad$ c) Nghiệm của bất phương trình $u(x) \leqslant v(x)$ là phần hoành độ tương ứng với phần đồ thị $y=u(x)$ nằm ở phía dưới so với phần đồ thị $y=v(x)$
$\quad$ d) Nghiệm của phương trình $u(x)=m$ là hoành độ giao điểm của đường thẳng $y=m$ với đồ thị $y=u(x)$
$\quad$ e) Bất phương trình $u(x) \geqslant m$ đúng với $\forall x \in I \Leftrightarrow \mathop {min}\limits_{x \in I} u(x) \geqslant m$
$\quad$ f) Bất phương trình $u(x) \leqslant m$ đúng với $\forall x \in I \Leftrightarrow \mathop {Max}\limits_{x \in I} u(x) \leqslant m$
$\quad$ g) Bất phương trình $u(x) \geqslant m$ có nghiệm $x \in I \Leftrightarrow \mathop {Max}\limits_{x \in I} u(x) \geqslant m$
$\quad$ h) Bất phương trình $u(x) \leqslant m$ có nghiệm $x \in I \Leftrightarrow \mathop {min}\limits_{x \in I} u(x) \leqslant m$
Lời giải.
a) Biến đổi phương trình $f(x)=0$ sao cho tham số $m$ nằm về một vế độc lập:
$$f(x) = m{x^2}+2mx-3 = 0 \Leftrightarrow m({x^2+2x}) = 3 \Leftrightarrow \frac{3}{x^2+ 2x}=m$$
Đặt $g(x):=\frac{3}{x^2 + 2x}=\frac{3}{(x+1)^2-1}=m$
Để $f(x)=0$ có nghiệm $x \in [1;2]$ thì $m$ phải lớn hơn hoặc bằng GTNN và nhỏ hơn hoặc bằng GTLN của hàm $g(x)$ trên đoạn $[1;2]$ (Xem "hằng đẳng thức" (d) và hình 1), tức là:
$$\mathop {min}\limits_{x \in [1;2]} g(x) \leqslant m \leqslant \mathop {Max}\limits_{x \in [1;2]} g(x)$$
Bây giờ xét hàm $g(x)$ trên $[1;2]$ tương tự như ở vấn đề 1, cụ thể như sau:
Vì $g(x) = \frac{3}{(x + 1)^2- 1}$ là hàm liên tục trên $[1;2]$, có đạo hàm $g'(x) = - \frac{2(x + 1)}{(x+1)^2-1} < 0,\forall x \in [1;2]$ nên $g(x)$ là hàm nghịch biến trên $[1;2]$.
Do đó,
$$ \mathop {min }\limits_{x \in [1;2]} g(x) = g(2) = \frac{3}{8}\\ \mathop {Max}\limits_{x \in [1;2]} g(x) = g(1) = 1$$
Kết luận: Giá trị $m$ thỏa mãn bài toán là: $\frac{3}{8} \leqslant m \leqslant 1$
b) Với $\forall x \in [1;4]$, ta có:
$$f(x) \leqslant 0 \Leftrightarrow m{x^2} + 2mx - 3 \leqslant 0\\ \Leftrightarrow m(x^2+2x) \leqslant 3\\ \Leftrightarrow g(x):= \frac{3}{x^2+2x} \geqslant m,\forall x \in [1;4]$$
Để $f(x) \leqslant 0$ nghiệm đúng với mọi $x \in [1;4]$ thì $g(x):= \frac{3}{x^2+2x} \geqslant m,\forall x \in [1;4]$, điều này có được khi $$\mathop {min }\limits_{x \in [1;4]} g(x) \geqslant m$$ (xem (e) và hình 1)
Vì hàm $g(x)$ liên tục và có đạo hàm $g'(x)=- \frac{2(x + 1)}{(x+1)^2-1} < 0$ trên đoạn [1;4] nên $g(x)$ là hàm nghịch biến trên $[1;4]$.
Do đó $\mathop {min }\limits_{x \in [1;4]} g(x) = g(4) = \frac{1}{8}$
Kết luận: Giá trị $m$ thỏa mãn bài toán là: $m \leqslant \frac{1}{8}$
b) Với $x \in [-1;3]$, ta có:
$$ f(x) \geqslant 0 \Leftrightarrow m({x^2+2x}) \geqslant 3 \Leftrightarrow m \geqslant \frac{3}{x^2+ 2x} \ \ (1) $$
Đặt và xét hàm số $g(x): = \frac{3}{x^2+2x},x \in [-1;3]$ (2)
Ở đây ta gặp chút rắc rối là đoạn $[-1;3]$ chứa điểm "đặc biệt" mà làm cho $g(x)$ không xác định là điểm $x=0$. Kỹ thuật là ta sẽ tách ra làm hai đoạn và đi xét riêng điểm $x=0$. Cụ thể:
Xét các khả năng sau:
$\bullet$ Nếu $x=0$, thay trực tiếp vào (1), bất phương trình trở thành $m.0=0 \geqslant 3$. Vô nghiệm!
$\bullet$ Nếu $x \in (0;3]$ thì
$$\text{bất phương trình đã cho } \Leftrightarrow g(x) \leqslant m \text{ có nghiệm } x \in (0;3] \Leftrightarrow \mathop {min}\limits_{x \in (0;3]} g(x) \leqslant m $$
Do $g\left( x \right) = \frac{3}{{{{\left( {x + 1} \right)}^2}}} - 1$ nghịch biến trên $(0;3]$ nên $\mathop {min}\limits_{x \in(0;3]} g(x) = g(3)= \frac{1}{5} \leqslant m$
$\bullet$ Nếu $x \in [-1;0)$ thì $x^2+2x<0$ n="" span="" style="font-family: arial, helvetica, sans-serif;" data-mce-style="font-family: arial, helvetica, sans-serif;">
$$ \text{bất phương trình đã cho }\Leftrightarrow g(x) \geqslant m \text{ có nghiệm }x \in [-1;0)\\ \Leftrightarrow \mathop {Max}\limits_{x \in [-1;0)} g(x) \geqslant m $$
Do $g(x)$ nghịch biến trên $[-1;0)$ nên $\mathop {Max}\limits_{x \in [-1;0)} g(x)=g(1) =- 3 \geqslant m$.
Kết hợp các trường hợp ta đi đến kết luận:
$$f(x) \geqslant 0 \text{ có nghiệm }x \in [-1;3] \Leftrightarrow m \in (-1;3] \cup [\frac{1}{5};+ \infty)$$
a) Biến đổi phương trình $f(x)=0$ sao cho tham số $m$ nằm về một vế độc lập:
$$f(x) = m{x^2}+2mx-3 = 0 \Leftrightarrow m({x^2+2x}) = 3 \Leftrightarrow \frac{3}{x^2+ 2x}=m$$
Đặt $g(x):=\frac{3}{x^2 + 2x}=\frac{3}{(x+1)^2-1}=m$
Để $f(x)=0$ có nghiệm $x \in [1;2]$ thì $m$ phải lớn hơn hoặc bằng GTNN và nhỏ hơn hoặc bằng GTLN của hàm $g(x)$ trên đoạn $[1;2]$ (Xem "hằng đẳng thức" (d) và hình 1), tức là:
$$\mathop {min}\limits_{x \in [1;2]} g(x) \leqslant m \leqslant \mathop {Max}\limits_{x \in [1;2]} g(x)$$
Bây giờ xét hàm $g(x)$ trên $[1;2]$ tương tự như ở vấn đề 1, cụ thể như sau:
Vì $g(x) = \frac{3}{(x + 1)^2- 1}$ là hàm liên tục trên $[1;2]$, có đạo hàm $g'(x) = - \frac{2(x + 1)}{(x+1)^2-1} < 0,\forall x \in [1;2]$ nên $g(x)$ là hàm nghịch biến trên $[1;2]$.
Do đó,
$$ \mathop {min }\limits_{x \in [1;2]} g(x) = g(2) = \frac{3}{8}\\ \mathop {Max}\limits_{x \in [1;2]} g(x) = g(1) = 1$$
Kết luận: Giá trị $m$ thỏa mãn bài toán là: $\frac{3}{8} \leqslant m \leqslant 1$
b) Với $\forall x \in [1;4]$, ta có:
$$f(x) \leqslant 0 \Leftrightarrow m{x^2} + 2mx - 3 \leqslant 0\\ \Leftrightarrow m(x^2+2x) \leqslant 3\\ \Leftrightarrow g(x):= \frac{3}{x^2+2x} \geqslant m,\forall x \in [1;4]$$
Để $f(x) \leqslant 0$ nghiệm đúng với mọi $x \in [1;4]$ thì $g(x):= \frac{3}{x^2+2x} \geqslant m,\forall x \in [1;4]$, điều này có được khi $$\mathop {min }\limits_{x \in [1;4]} g(x) \geqslant m$$ (xem (e) và hình 1)
Vì hàm $g(x)$ liên tục và có đạo hàm $g'(x)=- \frac{2(x + 1)}{(x+1)^2-1} < 0$ trên đoạn [1;4] nên $g(x)$ là hàm nghịch biến trên $[1;4]$.
Do đó $\mathop {min }\limits_{x \in [1;4]} g(x) = g(4) = \frac{1}{8}$
Kết luận: Giá trị $m$ thỏa mãn bài toán là: $m \leqslant \frac{1}{8}$
b) Với $x \in [-1;3]$, ta có:
$$ f(x) \geqslant 0 \Leftrightarrow m({x^2+2x}) \geqslant 3 \Leftrightarrow m \geqslant \frac{3}{x^2+ 2x} \ \ (1) $$
Đặt và xét hàm số $g(x): = \frac{3}{x^2+2x},x \in [-1;3]$ (2)
Ở đây ta gặp chút rắc rối là đoạn $[-1;3]$ chứa điểm "đặc biệt" mà làm cho $g(x)$ không xác định là điểm $x=0$. Kỹ thuật là ta sẽ tách ra làm hai đoạn và đi xét riêng điểm $x=0$. Cụ thể:
Xét các khả năng sau:
$\bullet$ Nếu $x=0$, thay trực tiếp vào (1), bất phương trình trở thành $m.0=0 \geqslant 3$. Vô nghiệm!
$\bullet$ Nếu $x \in (0;3]$ thì
$$\text{bất phương trình đã cho } \Leftrightarrow g(x) \leqslant m \text{ có nghiệm } x \in (0;3] \Leftrightarrow \mathop {min}\limits_{x \in (0;3]} g(x) \leqslant m $$
Do $g\left( x \right) = \frac{3}{{{{\left( {x + 1} \right)}^2}}} - 1$ nghịch biến trên $(0;3]$ nên $\mathop {min}\limits_{x \in(0;3]} g(x) = g(3)= \frac{1}{5} \leqslant m$
$\bullet$ Nếu $x \in [-1;0)$ thì $x^2+2x<0$ n="" span="" style="font-family: arial, helvetica, sans-serif;" data-mce-style="font-family: arial, helvetica, sans-serif;">
$$ \text{bất phương trình đã cho }\Leftrightarrow g(x) \geqslant m \text{ có nghiệm }x \in [-1;0)\\ \Leftrightarrow \mathop {Max}\limits_{x \in [-1;0)} g(x) \geqslant m $$
Do $g(x)$ nghịch biến trên $[-1;0)$ nên $\mathop {Max}\limits_{x \in [-1;0)} g(x)=g(1) =- 3 \geqslant m$.
Kết hợp các trường hợp ta đi đến kết luận:
$$f(x) \geqslant 0 \text{ có nghiệm }x \in [-1;3] \Leftrightarrow m \in (-1;3] \cup [\frac{1}{5};+ \infty)$$
$\quad$ Ví dụ sau đây tương tự như câu 1 của Ví dụ 4.2, cung cấp cho các bạn một kỹ thuật khi gặp khó khăn trong việc khẳng định tính đơn điệu của một hàm số bằng công cụ đạo hàm.
Ví dụ 4.2. Tìm $m$ để pt: $x\sqrt x +\sqrt{x+12}=m({\sqrt{5-x}+\sqrt{4-x}})$ có nghiệm.
Lời giải.
Điều kiện: $0 \leqslant x \leqslant 4$
Biến đổi phương trình đã cho và đặt hàm $f(x)$ như sau:
$$f(x): = \frac{x\sqrt x + \sqrt {x + 12}}{\sqrt {5 - x}+ \sqrt {4 - x} } = :\frac{u(x)}{v(x}=m$$
$\quad$ Việc tính đạo hàm $f(x)$ là khá phức tạp, tuy nhiên ta dễ suy ra $u(x)>0$ và là hàm tăng trên TXĐ, còn $v(x)>0$ và là hàm giảm (tức là $\frac{1}{v(x)}>0$ và là hàm tăng) trên TXĐ.
Suy ra $f(x) = \frac{u(x)}{v(x)}$ là một hàm số tăng trên đoạn $[0;4]$.
Như vậy:
$f(x)=m$ có nghiệm $\Leftrightarrow m \in \left[ {\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right);\mathop {Max}\limits_{x \in \left[ {0;4} \right]} f\left( x \right)} \right]$
$= \left[ {f\left( 0 \right);f\left( 4 \right)} \right]$
$= \left[ {2\left( {\sqrt {15} - \sqrt {12} } \right);12} \right]$
Kết luận: $m \in [2(\sqrt {15}- \sqrt {12});12]$
Điều kiện: $0 \leqslant x \leqslant 4$
Biến đổi phương trình đã cho và đặt hàm $f(x)$ như sau:
$$f(x): = \frac{x\sqrt x + \sqrt {x + 12}}{\sqrt {5 - x}+ \sqrt {4 - x} } = :\frac{u(x)}{v(x}=m$$
$\quad$ Việc tính đạo hàm $f(x)$ là khá phức tạp, tuy nhiên ta dễ suy ra $u(x)>0$ và là hàm tăng trên TXĐ, còn $v(x)>0$ và là hàm giảm (tức là $\frac{1}{v(x)}>0$ và là hàm tăng) trên TXĐ.
Suy ra $f(x) = \frac{u(x)}{v(x)}$ là một hàm số tăng trên đoạn $[0;4]$.
Như vậy:
$f(x)=m$ có nghiệm $\Leftrightarrow m \in \left[ {\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right);\mathop {Max}\limits_{x \in \left[ {0;4} \right]} f\left( x \right)} \right]$
$= \left[ {f\left( 0 \right);f\left( 4 \right)} \right]$
$= \left[ {2\left( {\sqrt {15} - \sqrt {12} } \right);12} \right]$
Kết luận: $m \in [2(\sqrt {15}- \sqrt {12});12]$
Ví dụ 4.3. Tìm $m$ để phương trình $3\sqrt{x-1}+m\sqrt{x+1}=2\sqrt[4]{x^2-1} \quad (1)$ có nghiệm thực.
Lời giải.
Điều kiện: $x \geqslant 1$
Biến đổi phương trình (1) và xét hàm $f(x)$ như sau:
$$f(x):= -3\sqrt{\frac{x-1}{x+1}}+2\sqrt[4]{\frac{x-1}{x+1}}=m \quad \quad (2)$$
Có thể đặt ẩn phụ $t=\sqrt[4]{\frac{x-1}{x+1}}=\sqrt[4]{{1-\frac{2}{x+1}}}$ thì $\sqrt {\frac{x - 1}{x + 1}} = {t^2}$, với $t \in [0;1)$.
Khi đó (2) trở thành: $g(t)=- 3{t^2}+3t=m$.
Đó là một hàm số bậc hai, việc khảo sát không có gì khó khăn!\par
Ta có $g'(t)=0 \Leftrightarrow t= \frac{1}{3}$.
Lập bảng biến thiên cho hàm $g(t)$ như sau:
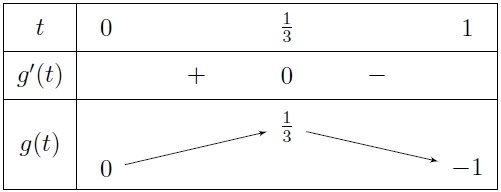
Nhìn vào bảng biến thiên dễ dàng suy ra giá trị của $m$ cần tìm là: $- 1< m \leqslant \frac{1}{3}$.
Ghi chú:
$\quad$ a) Đối với ẩn phụ $t$ ở trên, các bạn buộc phải tìm miền giá trị của nó, chớ có để sót bước này.
$\quad$ b)Bài toán này ở đề thi khối A-2007 và còn một số cách giải khác, các bạn tự tìm hiểu thêm!
Ghi chú:
$\quad$ a) Đối với ẩn phụ $t$ ở trên, các bạn buộc phải tìm miền giá trị của nó, chớ có để sót bước này.
$\quad$ b)Bài toán này ở đề thi khối A-2007 và còn một số cách giải khác, các bạn tự tìm hiểu thêm!
Ví dụ 4.4. Tìm $m$ để bất phương trình: $$m4^x+(m-1)2^{x+2}+m-1>0 \text{ đúng }\forall x \in \mathbb{R} \quad \quad (1)$$
Lời giải.
Đặt $2^x= t,t > 0$ thì (1) trở thành:
$$mt^2+ 4(m-1)t+m-1 > 0 \Leftrightarrow m(t^2+ 4t + 1) > 4t + 1\\ \Leftrightarrow \frac{4t + 1}{t^2 + 4t + 1} < m$$
Đặt $g(t): = \frac{4t + 1}{t^2 + 4t + 1}$ với $t>0$.
Khi đó (1) đúng với $\forall x \in \mathbb{R}$ khi và chỉ khi $g(t)
Dễ thấy $g(t)$ là hàm nghịch biến trên $[0; + \infty)$, theo "hằng đẳng thức" (f) thì$$\text{yêu cầu của bài toán} \Leftrightarrow \mathop {Max}\limits_{t \in [0; + \infty)} g(t) < m\\ \Leftrightarrow g(0) < m\\ \Leftrightarrow 1 < m $$
Kết luận: $\boxed{m > 1}$
Lời giải.
Đặt $2^x= t,t > 0$ thì (1) trở thành:
$$mt^2+ 4(m-1)t+m-1 > 0 \Leftrightarrow m(t^2+ 4t + 1) > 4t + 1\\ \Leftrightarrow \frac{4t + 1}{t^2 + 4t + 1} < m$$
Đặt $g(t): = \frac{4t + 1}{t^2 + 4t + 1}$ với $t>0$.
Khi đó (1) đúng với $\forall x \in \mathbb{R}$ khi và chỉ khi $g(t)
Dễ thấy $g(t)$ là hàm nghịch biến trên $[0; + \infty)$, theo "hằng đẳng thức" (f) thì$$\text{yêu cầu của bài toán} \Leftrightarrow \mathop {Max}\limits_{t \in [0; + \infty)} g(t) < m\\ \Leftrightarrow g(0) < m\\ \Leftrightarrow 1 < m $$
Kết luận: $\boxed{m > 1}$
Ví dụ 4.5. Tìm $m$ để hệ phương trình sau có nghiệm: $\left\{ \begin{gathered} x+\frac{1}{x}+y+ \frac{1}{y}=5 \\ x^3+ \frac{1}{x^3}+y^3+ \frac{1}{y^3} = 15m-10 \\ \end{gathered} \right. \quad \,(1)$
$\quad$ Nhận định: Đây là hệ đối xứng loại I, nếu đề bài yêu cầu giải hệ thì bài toán đơn giản, song ở đây xuất hiện $m$ và yêu cầu tìm giá trị $m$ để hệ có nghiệm. Nhiều bạn sẽ chọn cách đặt ẩn phụ và cố gắng biến đổi sao cho sử dụng được Định lý Viète rồi biện luận theo $m$.
$\quad$ Lời giải sau cũng đi theo hướng đó nhưng bước cuối cùng lại rẽ sang hướng khác!
Lời giải.
Đặt $u: = x + \frac{1}{x}$ và $v: = y + \frac{1}{y}$.
Khi đó:
\[\left| u \right| = \left| {x + \frac{1}{x}} \right| = \left| x \right| + \left| {\frac{1}{x}} \right| \geqslant 2\sqrt {\left| x \right|\left| {\frac{1}{x}} \right|} = 2\]
Tương tự ta cũng tìm được: $|v| \geqslant 2$
Ta lại có:
$$ x^3+ \frac{1}{x^3} = {(x + \frac{1}{x})^3} - 3x^2.\frac{1}{x} - 3x.({\frac{1}{x}})^2$$
$$ = {({x + \frac{1}{x}})^3} - 3( {x + \frac{1}{x}})\\ = {u^3} - 3u$$
Tương tự, ${y^3} + \frac{1}{y^3}={v^3} - 3v$
Thay vào hệ (1):
Đặt $u: = x + \frac{1}{x}$ và $v: = y + \frac{1}{y}$.
Khi đó:
\[\left| u \right| = \left| {x + \frac{1}{x}} \right| = \left| x \right| + \left| {\frac{1}{x}} \right| \geqslant 2\sqrt {\left| x \right|\left| {\frac{1}{x}} \right|} = 2\]
Tương tự ta cũng tìm được: $|v| \geqslant 2$
Ta lại có:
$$ x^3+ \frac{1}{x^3} = {(x + \frac{1}{x})^3} - 3x^2.\frac{1}{x} - 3x.({\frac{1}{x}})^2$$
$$ = {({x + \frac{1}{x}})^3} - 3( {x + \frac{1}{x}})\\ = {u^3} - 3u$$
Tương tự, ${y^3} + \frac{1}{y^3}={v^3} - 3v$
Thay vào hệ (1):
\[\left\{ \begin{gathered} u + v = 5 \\ {u^3} + {v^3} - 3\left( {u + v} \right) = 15m - 10 \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 5 \\ uv = 8 - m \\\end{gathered} \right.\]
Suy ra $u, v$ phải là nghiệm của phương trình bậc hai $g(t):=t^2-5t+8=m$
Như vậy, hệ phương trình (1) có nghiệm khi và chỉ khi phương trình
$g(t)=m$ có hai nghiệm $t_1, t_2$ sao cho $|{t_1}| \geqslant 2$ và $|{t_2}| \geqslant 2$.
$\quad$ Bây giờ công việc còn lại là khảo sát hàm số $g(t)$ trên tập $D = \mathbb{R} \backslash (-2;2)$.
Ta sẽ nhìn thấy kết quả của việc khảo sát hàm $g(t)$ qua bảng biến thiên sau:
Suy ra $u, v$ phải là nghiệm của phương trình bậc hai $g(t):=t^2-5t+8=m$
Như vậy, hệ phương trình (1) có nghiệm khi và chỉ khi phương trình
$g(t)=m$ có hai nghiệm $t_1, t_2$ sao cho $|{t_1}| \geqslant 2$ và $|{t_2}| \geqslant 2$.
$\quad$ Bây giờ công việc còn lại là khảo sát hàm số $g(t)$ trên tập $D = \mathbb{R} \backslash (-2;2)$.
Ta sẽ nhìn thấy kết quả của việc khảo sát hàm $g(t)$ qua bảng biến thiên sau:
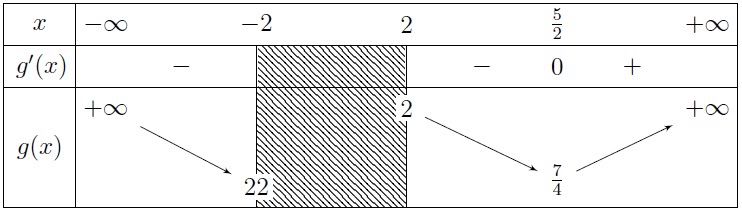
Kết luận: Hệ (1) có nghiệm $ \Leftrightarrow \frac{7}{2} \leqslant m \leqslant 2$ hoặc $m \geqslant 22$.
Bài tập 4.1. Tìm $m$ để bất phương trình: $-x^3+3mx-2 < -\frac{1}{x^3}$ nghiệm đúng $\forall x \geqslant 1$
Bài tập 4.2. Tìm $m$ để bất phương trình: $x^3+3{x^2}-1 \leqslant m({\sqrt x}-\sqrt {x-1})^3$ có nghiệm.
Bài tập 4.3. Tìm $m$ để bất phương trình: $\sqrt {(4+x)(6-x)} \leqslant {x^2} - 2x + m$ nghiệm đúng $\forall x \in [-4;6]$
Bài tập 4.4. Tìm $m$ để bất phương trình: $\sqrt {3+x}+ \sqrt {6-x}- \sqrt {18+3x-x^2} \leqslant {m^2}-m+1$ đúng $\forall x \in [-3;6]$.
Bài tập 4.5. Tìm $m$ để phương trình: $\sqrt {3 + x} + \sqrt {6 - x} - \sqrt {18 + 3x - {x^2}} = m$ có nghiệm.
Bài tập 4.6. Chứng minh rằng: Với mọi $m>0$ phương trình ${x^2} + 2x - 8 = \sqrt {m\left( {x - 2} \right)} $ luôn có đúng hai nghiệm phân biệt.
Bài tập 4.7. Tìm $m$ để phương trình: $\root 4 \of {2x}+ \sqrt {2x}+2\root 4 \of {6-x}+2\sqrt {6-x}=m$ có đúng hai nghiệm thực phân biệt.
Bài tập 4.8. Tìm $x$ để bất phương trình: $x^2+2x(\sin y+\cos y)+1\geqslant 0$ đúng với $\forall y \in \mathbb{R}$
Bài tập 4.9.(A-2002). Tìm $m$ để phương trình: $\log _3^2x + \sqrt {\log _3^2x + 1} - 2m - 1 = 0$ có ít nhất một nghiệm thuộc đoạn $[1;3^{\sqrt 3 }]$

0 comments:
Đăng nhận xét