Bài toán 1
Xem Trái Đất như một khối cầu tâm $O$.
Điểm $S$ có tọa độ $11^o$ vĩ Bắc, $106^o30'$ kinh Đông.
Điểm $P$ có tọa độ $49^o$ vĩ Bắc, $2^o30'$ kinh Đông.
Tính số đo góc $\widehat{POS}$ ?
Giải
Phương trình tham số của mặt cầu Trái Đất là:
$$\begin{cases}x=R\cos \varphi \cos \lambda \\ y = R\cos \varphi \sin \lambda \\ z = R \sin \varphi \end{cases}$$
Trong đó $\varphi $ là vĩ độ (mang dấu dương khi điểm đang xét ở Bán cầu Bắc, mang dấu âm khi ở Bán cầu Nam), $\lambda$ là kinh độ (mang dấu dương khi ở Bán cầu Đông, dấu âm khi ở Bán cầu Tây)
Ta có tọa độ của $S,P$ là
$$S(R\cos \varphi_S \cos \lambda_S ; R\cos \varphi_S \sin \lambda_S ; R \sin \varphi_S), \quad P(R\cos \varphi_P \cos \lambda_P ; R\cos \varphi_P \sin \lambda_P ; R \sin \varphi_P)$$
$$\overrightarrow{OP}.\overrightarrow{OS}=R^2 \left [ \cos \varphi_P \cos \varphi_S \cos (\lambda_P - \lambda_S) +\sin \varphi_P\sin \varphi_S \right ]$$
\begin{equation} \label{eq:1} \boxed{\cos \left ( \overrightarrow{OP}, \overrightarrow{OS} \right ) = \frac{\overrightarrow{OP}. \overrightarrow{OS}}{OP.OS} = \cos \varphi_P \cos \varphi_S \cos (\lambda_P - \lambda_S) +\sin \varphi_P\sin \varphi_S} \end{equation}
Theo bài, $\varphi_S = 11^o, \lambda_S = 106,5^o, \varphi_P=49^o, \lambda_P=2,5^o$, ta có:
$$\cos \left ( \overrightarrow{OP}, \overrightarrow{OS} \right ) = \cos 49^o \cos 11^o \cos 104^o + \sin 11^o \sin 49^o \approx -0,01179$$
Vậy $\widehat{POS} \approx 90^o40’32’’$
Bài toán 2
Tính diện tích phần bề mặt Trái Đất giới hạn bởi các vĩ tuyến $11^o$ Bắc, $49^o$ Bắc và các kinh tuyến $2^o30'$ Đông, $106^o30'$ Đông ?
Giải
Trước hết ta tìm công thức tính diện tích phần mặt cầu giới hạn bởi hai đường vĩ tuyến. (Người ta gọi là hình đớt cầu)
Dễ thấy hình đớt cầu là mặt tròn xoay có được nhờ quay hình phẳng giới hạn bởi các đường sau xung quanh trục $Ox$:
$$y=\sqrt{R^2-x^2} \quad \text{(nửa đường tròn tâm O phía trên trục hoành)}, \quad x = a, x = b, \quad (0<a<b \leq R)$$
Áp dụng công thức:
$$S = 2\pi\int_{a}^{b}y\sqrt{1+(y')^2}dx$$
Ta có:
\begin{equation} \label{eq:2} S_{(R,a,b)}=2\pi\int_{a}^{b}\sqrt{R^2-x^2}\sqrt{1+\frac{x^2}{R^2-x^2}}dx = 2\pi\int_{a}^{b}Rdx = 2\pi R (b-a) \end{equation}
Quay lại với Trái đất, Diện tích hình đớt cầu giới hạn bởi hai đường vĩ tuyến $\varphi_1$ và $\varphi_2, (\varphi_1 < \varphi_2)$. Ta lấy $a=R\sin \varphi_1, b = R\sin \varphi_2$. Ta được
$$S_{(R,\sin \varphi_1,\sin \varphi_2)}=2\pi R^2 (\sin \varphi_2- \sin \varphi_1)$$
Gọi $S_{(\varphi_1; \varphi_2; \lambda_1; \lambda_2)}$ là diện tích cần tìm. Dễ thấy đó là diện tích phần phần đớt cầu giới hạn bởi hai kinh tuyến $\lambda_1$ và $\lambda_2$. Ta có:
\begin{equation} \label{eq:3} \boxed{ S_{(\varphi_1; \varphi_2; \lambda_1; \lambda_2)}=\frac{|\lambda_2-\lambda_1|}{360} \times 2\pi R^2 (\sin \varphi_2- \sin \varphi_1) } \end{equation}
Lấy $R=6370 km, \varphi_1 = 11^o, \varphi_2=49^o, \lambda_1 = 2^o30', \lambda_2 = 106^o30'$, ta có $S\approx 41 \ 532 \ 886,63 km^2$
Bài toán 3
Điểm $A$ có tọa độ $\varphi _A=11^o$ ; $\lambda _A=2^o30'$ ($11^o$ vĩ Bắc, $2^o30'$ kinh Đông)
Điểm $B$ có tọa độ $\varphi _B=49^o$ ; $\lambda _B=106^o30'$ ($49^o$ vĩ Bắc, $106^o30'$ kinh Đông)
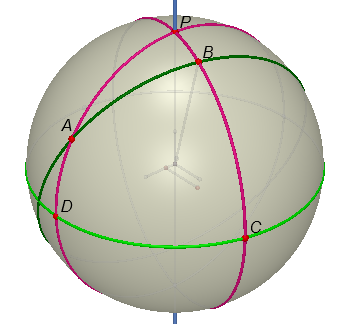
Giả sử trên bề mặt Trái Đất, người ta nối 2 thành phố $A$ và $B$ bằng 1 đường ngắn nhất (gọi là đường $(L)$)
Tính diện tích bề mặt Trái Đất giới hạn bởi đường $(L)$, các đường kinh tuyến đi qua $A$ và $B$ và đường xích đạo ?
Giải
1) Diện tích cần tìm là
$$S_{ABCD}=S_{CPD} - S_{PAB}$$
Trong đó $P$ là điểm cực Bắc. $C,D$ lần lượt là giao điểm của kinh tuyến $\lambda_B, \lambda_A$ với đường xích đạo.
2) Để tính $S_{PAB}$. Ta cần đi tìm công thức tính diện tích tam giác trên mặt cầu.
Định nghĩa:
Tam giác cầu $ABC$ là Tam giác nằm trên trên mặt cầu, các đường cong đi qua AB, BC, CA là các đường tròn lớn của mặt cầu.
Kí hiệu $A$ là góc giữa hai mặt phẳng $(AOB)$ và $(AOC)$.
$A$ đo bằng radian.
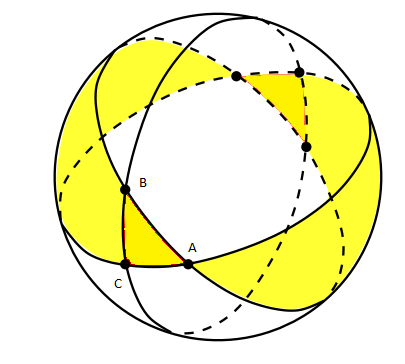
Khi đó gọi $S_A$ là diện tích phần mặt cầu giới hạn bởi hai mặt phẳng $(OAB)$ và $(OAC)$ (phần tô vàng)
Gọi $S$ là diện tích mặt cầu tâm $O$ bán kính $R$,
$S=4\pi R^2$.
Ta có:
$$S_A = 2 \times \frac{S}{2 \pi}\times A = 4A\times R^2$$
3) Ta chứng minh định lý Girard:
Nếu $ABC$ là một tam giác cầu thì Diện tích tam giác $ABC$ được tính bằng công thức:
\begin{equation} \label{eq:4} \boxed{S_{ABC} = R^2(A+B+C-\pi)} \end{equation}
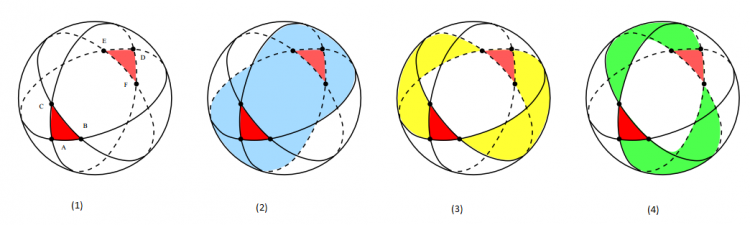
Thật vậy, Tam giác $ABC$ và tam giác $DEF$ (là hai tam giác bằng nhau) giúp ta chia mặt cầu thành các phần dưới đây:
Gọi $S_{2}, S_3, S_4$ lần lượt là diện tích các phần $(2), (3), (4)$.
Dễ thấy: các phần $(2), (3), (4)$ phủ kín mặt cầu và tam giác $ABC$ được đếm lặp $6$ lần. Tức là thừa $4$ lần. Do đó:
$$\begin{align*} & S = S_2+S_3+S_4-4S_{ABC} \\ \iff & 4\pi R^2 = 4A.R^2+4B.R^2+4C.R^2 – 4S_{ABC} \\ \iff & S_{ABC} = (A+B+C-\pi)R^2 \quad \text{(đpcm)}\end{align*}$$
4) Bây giờ cần tìm các góc $A, B, P$ của tam giác $PAB$.
Dễ thấy $P = |\lambda_A - \lambda_B| = 104^o = \frac{26\pi}{45}$
5) Để tính được các góc $A,B$, ta cần đi chứng minh Định lý cosin thứ nhất.
Định lý cosin thứ nhất.
Cho tam giác cầu $ABC$ nằm trên mặt cầu đơn vị (bán kính bằng 1). Đặt $a=\widehat{BOC}, b= \widehat{AOC}, c= \widehat{AOB}$. Khi đó:
\begin{equation} \label{eq:5} \boxed{\cos A = \dfrac{\cos a - \cos b \cos c}{\sin b \sin c}} \end{equation}
Chứng minh:
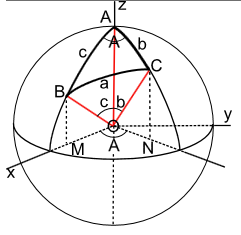
Chọn hệ tọa độ $Oxyz$ sao cho $A \in Oz, B \in (xOz)$.
Khi đó:
$$A(0;0;1), \quad B(\sin c; 0; \cos c), \quad C(\sin b \cos A; \sin b \sin A; \cos b)$$
Khi đó
$$\cos a = \overrightarrow{OB}.\overrightarrow{OC} = \sin c \sin b \cos A + \cos c \cos b$$
Do đó ta có đpcm.
6) Đối với tam giác $PAB$, ta có $b =90^o - \varphi_A =79^o, a= 90^o-\varphi_B = 41^o$.
Áp dụng công thức $\eqref{eq:1}$, ta thu được
$$p = \widehat{AOB} \approx 90^o40’32’’$$
Áp dụng định lý cosin thứ nhất cho tam giác $PAB$ ta có:
$$\cos A = \dfrac{\cos a - \cos b \cos p}{\sin b \sin p} \approx 0,771180674$$
Suy ra $A \approx 0,690 102 644 3 \quad (rad)$
$$\cos B = \dfrac{\cos b - \cos a \cos p}{\sin a \sin p} \approx 0,3044256591$$
Suy ra $B \approx 1,261 460 915 \quad (rad)$
Áp dụng định lý định lý Girard ta có:
$$S_{PAB} = (P+A+B- \pi)R^2$$
Do đó
$$S_{ABCD}=S_{CPD} - S_{PAB} = P.R^2 - (P+A+B- \pi)R^2 = (\pi – A – B )R^2 \approx 48 \ 287 \ 691,56 \ km^2$$
(Quái lạ, sao nó có vẻ không đúng lắm so với Google Earth)
Lấy $R=6371$ thì sẽ được $S \approx 48 \ 302 \ 853. 72 \ km^2$
(kết quả này gần với thực tế hơn.

0 comments:
Đăng nhận xét