Mặt Trời, Mặt Trăng và Lượng giác

Mặt Trời cách Mặt Trăng bao xa? Mặt Trời lớn hơn Mặt Trăng bao nhiêu lần? Và làm thế nào để trả lời các câu hỏi đó nếu bạn là một người Hy Lạp cổ đại, kẻ thậm chí không có lấy 1 chiếc kính thiên văn?

Nếu bạn là Aristarchus (Aristarchus of Samos), người đã sống vào khoảng 2300 năm trước, khi đó, bạn sẽ dựa vào chuyên môn hình học tuyệt vời của mình, kết hợp với một nhận thức quan trọng, đó là Mặt Trăng tỏa sáng vào ban đêm vì nó được chiếu sáng bởi Mặt Trời. Không giống như nhiều người, Aristarchus nhận ra rằng Trái Đất chuyển động xung quanh Mặt Trời.

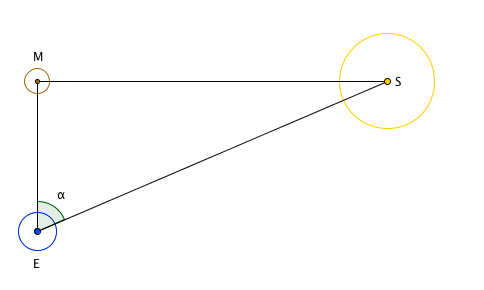
Được trang bị kiến thức Mặt Trời chiếu sáng Mặt Trăng, Aristarchus nhận ra rằng ở một nửa Mặt Trăng, tam giác hình thành bởi Trái Đất ($E$), Mặt Trăng ($M$) và Mặt Trời ($S$) có một góc vuông tại $M$.

Bạn có thể thuyết phục mình về điều này bằng cách tưởng tượng Mặt Trời ở những nơi khác nhau trong sơ đồ trên và kiểm tra rằng các tia sáng song song phát ra từ nó chiếu sáng đúng một nửa của Mặt Trăng (nhìn từ Trái Đất) chỉ khi có một góc vuông tại $M$.

Aristarchus đã đo khoảng cách tương đối của Mặt Trời và Mặt Trăng bằng cách đo tỉ lệ $\frac{ES}{EM}$, trong đó $ES$ là khoảng cách từ Trái Đất đến Mặt Trời và $EM$ là khoảng cách từ Trái Đất đến Mặt Trăng. Bằng lượng giác, bạn biết rằng

$$\frac{EM}{ES} = \cos \alpha$$

trong đó $\alpha $ là giá trị góc $E$ của tam giác. Vì thế

$$\frac{ES}{EM} = \frac{1}{\cos\alpha}$$

Ngày nay, ta có thể ước tính $\alpha = 89.85^\circ $ ta được:

$$\frac{ES}{EM} = \frac{1}{\cos 89.85^\circ} \approx 382. $$

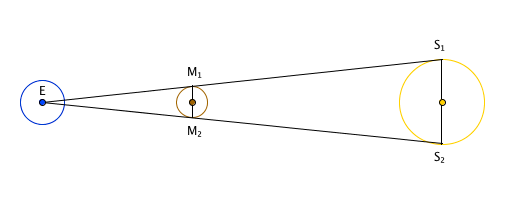
Vì vậy, Mặt Trời xa Trái Đất hơn gần $400$ lần so với Mặt Trăng. Aristarchus cũng nhận thấy rằng trong một nhật thực toàn phần, Mặt Trăng che kín hoàn toàn Mặt Trời. Điều này cho chúng ta sơ đồ sau:

Sử dụng thực tế đó và tỷ lệ giữa $ ES_1 $ và $ EM_1 $ bằng tỷ lệ giữa $ S_1S_2 $ và $ M_1M_2 $ (vì chúng chúng nằm trong cặp tam giác đồng dạng) chúng ta có thể suy luận rằng đường kính của Mặt Trời là lớn hơn khoảng $400$ lần hơn đường kính của Mặt Trăng.

Kết quả Aristarchus đã đưa ra khác xa với kết quả trên. Ông ước tính Mặt Trời lớn hơn khoảng từ 18 đến 20 Mặt Trăng. Điều này một phần là vì ông không có phương tiện để đo góc $ \alpha $ đủ chính xác và ước tính nó bằng $ 87^\circ. $ Sử dụng giá trị này trong tính toán trên, ông cho rằng Mặt Trời lớn hơn khoảng $19$ Mặt Trăng: một sự thay đổi nhỏ trong một góc $\alpha $ gần $ 90 ^\circ $ dẫn đến một sự thay đổi lớn trong $\frac{1}{\cos {\alpha}} $.

Lý do tại sao Aristarchus chỉ có thể đưa ra phạm vi $18-20$, chứ không phải một số chính xác, đó là lượng giác thời đó chưa phát triển. Ông không có khái niệm về côsin, hiển nhiên không có bảng giá trị lượng giác. Thay vào đó, ông đã phải sử dụng một lập luận hình học phức tạp hơn để đến với câu trả lời gần đúng của mình. Đây là một dẫn chứng cho khẳng định lượng giác rất hữu ích cho các nhà thiên văn học.

 Theo Plus.math.org