Chia đôi diện tích tứ giác lồi

Anh Đạt có đưa cho em bài toán sau:

Bài toán 1

Cho tứ giác lồi $ABCD$. Hãy vẽ đường thẳng đi qua $A$ và chia tứ giác thành hai phần có diện tích bằng nhau.

Giải

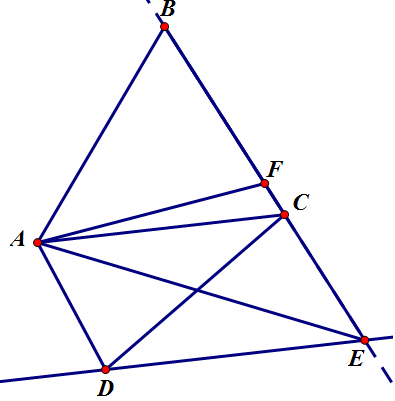
a) Phân tích: Giả sử đã dựng được đường thẳng $\Delta$ thỏa mãn yêu cầu bài toán. Đường thẳng $\Delta$ cắt $BC$ hoặc $CD$ tại $F$.

Qua $D$ dựng đường thẳng $d$ song song với $AC$; $BC$ cắt $d$ tại $E$.

Dễ thấy:

$$S_{ACD}=S_{ACE}\Rightarrow S_{ABCD} = S_{ABE}$$

Bài toán trở thành tìm điểm $G$ trên cạnh $BE$ sao cho $AG$ chia đôi diện tích tam giác $ABE$. Dễ thấy khi đó $G$ là trung điểm $BE$.

Từ đó nếu $G$ thuộc đoạn $BC$ thì $G\equiv F$, nếu $G$ thuộc đoạn $CE$ thì $AG \cap CD = F$

b) Cách dựng:

Qua $D$ dựng đường thẳng $d$ song song với $AC$; $BC$ cắt $d$ tại $E$.

Dựng trung điểm $G$ của $BE$.

Nếu $G$ thuộc đoạn $BC$ thì $G\equiv F$, nếu $G$ thuộc đoạn $CE$ thì qua $B$ dựng đường thẳng $d'$ song song với $AC$; $CD$ cắt $d'$ tại $E'$.
Điểm $F$ khi đó là trung điểm $DE'$

c) Chứng minh:

Ta có:

$$S_{ABF}=S_{AFE}=S_{AFC}+S_{ACE}=S_{AFC}+S_{ACD}=S_{ADCF}$$

(đpcm)

d) Biện luận: Bài toán có đúng một nghiệm hình.