Bài toán:
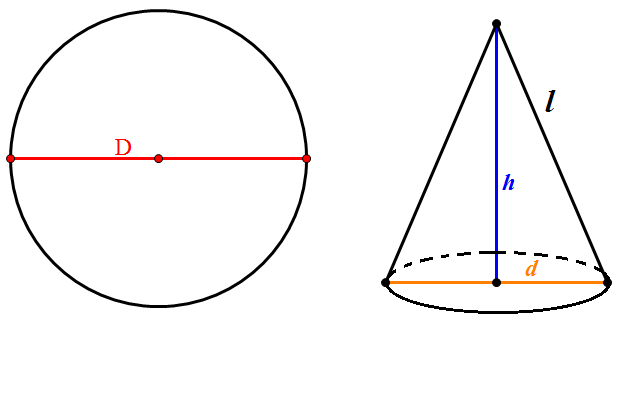
Cho một miếng inox hình tròn có đường kính $D$. Cần phải cắt miếng inox đó như thế nào để có thể tạo ra một hình nón có đường kính đáy là $d$, chiều cao là $h$.
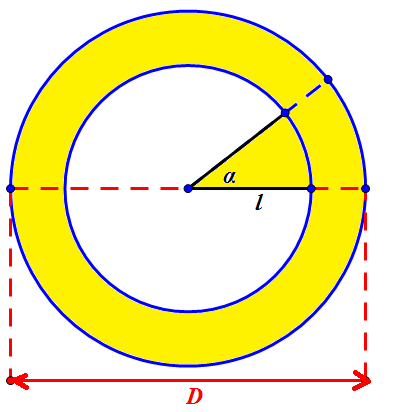
Giả sử đoạn ta cần căt bỏ là phần được tô màu vàng trên hình vẽ.
Đường sinh của hình nón cần làm là:
$$l = \sqrt{h^2+\left(\frac{d}{2}\right)^2}$$
Đường sinh đó chính là bán kính của hình quạt $A$ và độ dài cung tròn của $A$ cũng bằng chu vi đáy hình nón. Do đó:
$$l(2\pi - \alpha) = d\pi \Leftrightarrow \alpha = \frac{\pi(2l-d)}{l}$$
$$l(2\pi - \alpha) = d\pi \Leftrightarrow \alpha = \frac{\pi(2l-d)}{l}$$
Công thức trên, $\alpha$ được đo bằng radian. Do đó, công thức theo đơn vị độ là:
$$\alpha = \frac{2l - d}{l} \times 180^o $$
$$\alpha = \frac{2l - d}{l} \times 180^o $$
Cảm ơn Admin đã chia sẻ bài viết hay.
......................................................
Cơ sở sản xuất nón bucket giá rẻ Bàn Tay Việt
nón bucket giá sỉ.